Beispiel 174 - Zuordnen - 4 Ableitungen zu 4 Funktionen; 10 Graphen

Übungstyp und Quelle

Übungstyp

Auswählen

Vorhandene Strukturelemente

Nummerierung / Kennzeichnung von Beispielen

Aus dem Schulbuch

195789

Seite(n)

212

Original

Aufbereitet

Um schnelles Arbeiten zu ermöglichen, alle Koordinatensysteme gemeinsam nur einmal beschreiben, die Ankreuzoption gleichzeitig mit der Beschreibung anbieten.

Sind Funktionen und die (1.) Ableitungen angegeben, müssen:

bei der Funktion die Wendestellen und Extremstellen,

bei den (1.) Ableitungen die Extremstellen und Nullstellen angegeben sein.

Bei geschätzten Werten sowohl bei den Funktionen als auch bei 1. Ableitungen unbedingt die gleichen Stellen angeben.

Zuerst die Beschreibung des Graphen, dann die Angaben der Punkte.

+++950 |AN 3.2|

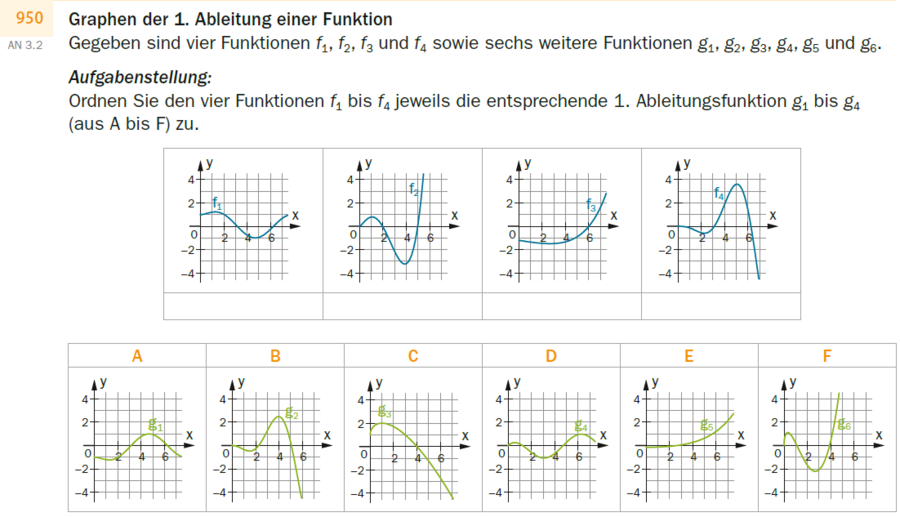
Graphen der 1. Ableitung einer Funktion

Gegeben sind vier Funktionen f_1, f_2, f_3 und f_4 sowie sechs weitere Funktionen g_1, g_2, g_3, g_4, g_5 und g_6.

---

Aufgabenstellung:

Ordnen Sie den vier Funktionen f_1 bis f_4 jeweils die entsprechende 1. Ableitungsfunktion g_1 bis g_6 (aus A bis F) zu.

{{Ableitungsfunktionen g_1 bis g_4, A bis F:}}

{{Grafik: 10 Koordinatensysteme:

waagrechte Achse: x; [0; 6], Skalierung: 1;

senkrechte Achse: y; [-4; 4], Skalierung: 1;

---

Ableitungsfunktionen g_1 bis g_6 (A bis F):

A: der dargestellte Graph von g_1 beginnt linksgekrümmt fallend bei ~~(0|-1), hat im 4. Quadranten ein lokales Minimum (Tiefpunkt), im 1. Quadranten ein lokales Maximum (Hochpunkt) und endet rechtsgekrümmt fallend im 4. Quadraten. Charakteristische Wertepaare (ungefähre Werte): T (1,5|-1,2); N_1 (3|0); H (4,5|1); N_2 (6|0)

---

B: der dargestellte Graph von g_2 beginnt linksgekrümmt fallend im Ursprung, hat im 4. Quadranten ein lokales Minimum (Tiefpunkt), im 1. Quadranten ein lokales Maximum (Hochpunkt) und endet rechtsgekrümmt fallend im 4. Quadraten. Charakteristische Wertepaare (ungefähre Werte): T (2|-0,8); N_1 (2|0); H (4|2,5); N_2 (5|0)

---

C: der dargestellte Graph von g_3 ist rechtsgekrümmt. Er beginnt steigend bei ~~(0|1,6), hat ein lokales Maximum (Hochpunkt) im 1. Quadranten und endet fallend im 4. Quadranten. Charakteristische Wertepaare (ungefähre Werte): H (1|2); N (4|0)

---

D: der dargestellte Graph von g_4 beginnt rechtsgekrümmt steigend im Ursprung, hat ein lokales Maximum (Hochpunkt) im 1. Quadranten, ein lokales Minimum (Tiefpunkt) im 4. Quadranten, ein lokales Maximum (Hochpunkt) im 1. Quadranten und endet rechtsgekrümmt fallend. Charakteristische Wertepaare (ungefähre Werte): H (0,5|0,1); N_1 (1,5|0); T (3|-1); N_2 (4,5|0); H (6|1)

---

E: der dargestellte Graph von g_5 beginnt bei ~~(0|-0,1), schneidet bei (2|0) die waagrechte Achse ist linksgekrümmt steigend und endet im 1. Quadranten.

---

F: der dargestellte Graph von g_6 beginnt rechtsgekrümmt steigend im Ursprung, hat ein lokales Maximum (Hochpunkt) im 1. Quadranten, ein lokales Minimum (Tiefpunkt) im 4. Quadranten und endet linksgekrümmt steigend im 1. Quadranten. Charakteristische Wertepaare (ungefähre Werte): N_1 (0|0); H (0,3|1); N_2 (1|0); T (2,5|-2,1); N_3 (3,8|0);

---

Funktionen f_1 bis f_4 mit Zuordnungsmöglichkeit

[] der dargestellte Graph von f_1 beginnt rechtsgekrümmt steigend bei (0|1), hat ein lokales Maximum (Hochpunkt) im 1. Quadranten, ein lokales Minimum (Tiefpunkt) im 4. Quadranten und endet linksgekrümmt steigend im 1. Quadranten. Charakteristische Wertepaare (ungefähre Werte): H (1,5|1,2); N =W (3|0); T (4,5|-1); N_3 (6|0);

[] der dargestellte Graph von f_2 beginnt rechtsgekrümmt steigend bei (0|0), hat ein lokales Maximum (Hochpunkt) im 1. Quadranten, ein lokales Minimum (Tiefpunkt) im 4. Quadranten und endet linksgekrümmt steigend im 1. Quadranten. Charakteristische Wertepaare (ungefähre Werte): H (1|1); N_1 (2|0); W_1 (2,5|-2); T (3,8|-3,3); N_3 (5|0);

[] der dargestellte Graph von f_3 ist linksgekrümmt. Er beginnt bei ~~(0|-1,1) fallend, hat im 4. Quadranten ein lokales Minimum (Tiefpunkt) und endet steigend im 1. Quadranten. Charakteristische Wertepaare(ungefähre Werte): T (3|-1,5); N (6|0);

[] der dargestellte Graph von f_4 beginnt rechtsgekrümmt fallend im Ursprung, hat im 4. Quadranten ein lokales Minimum (Tiefpunkt), im 1. Quadranten ein lokales Maximum (Hochpunkt) und endet rechtsgekrümmt fallend im 4. Quadraten. Charakteristische Wertepaare (ungefähre Werte): W_1 (1|-0,1); T_1(2|--0,5); N (3|0); W_2(4|2); H (5|3,5); N_2 (6,2|0)}}

-----