Beispiel 166 - Interpretieren - geeignete Wertepaare zur Erstellung einer Polynomfunktion finden
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 194
Original
Aufbereitet
Verlauf möglichst knapp beschreiben, bevorzugt Punkte mit ganzzahligen Koordinaten und charakteristische Wertepaare (Extremwerte, Wendepunkte …).
Immer auch auf die Aufgabenstellung achten: Wenn nur die 4 wichtigen Punkte angegeben werden, müsste die Beschreibung nur kopiert werden. Daher bitte eine Verlaufsbeschreibung mit mehr als 4 Punkten verwenden.
+++862 |FA 4.2|
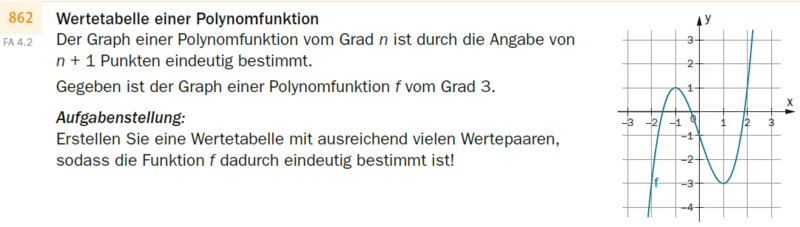
Wertetabelle einer Polynomfunktion
Der Graph einer Polynomfunktion vom Grad n ist durch die Angabe von n +1 Punkten eindeutig bestimmt.
Gegeben ist der Graph einer Polynomfunktion f vom Grad 3.
{{Grafik: Koordinatensystem:
waagrechte Achse: x; [-3; 3], Skalierung: 1;
senkrechte Achse: y; [-4; 3], Skalierung: 1;
---
Der dargestellte Graph von f ist punktsysmmetrisch zu (0|-1). Er beginnt steigend und rechtsgekrümmt im 3. Quadranten, hat ein lokales Maximum (Hochpunkt) bei (-1|1), einen Wendepunkt bei (0|-1), ein lokales Minimum (Tiefpunkt) bei (1|-2) und endet steigend und linksgekrümmt im 1. Quadranten. Weitere Wertepaare sind: (-2|-3); (2|1).}}
---
Aufgabenstellung:
Erstellen Sie eine Wertetabelle mit ausreichend vielen Wertepaaren, sodass die Funktion f dadurch eindeutig bestimmt ist!
[]
-----