Beispiel 165 - Multiple Choice - Potenzfunktionen; 5 Funktionen in 5 Koordinatensystemen mit Skalierung

Übungstyp und Quelle

Übungstyp

Auswählen

Vorhandene Strukturelemente

Nummerierung / Kennzeichnung von Beispielen

Aus dem Schulbuch

195789

Seite(n)

191

Original

Aufbereitet

Um die Orientierung und das schnelle Arbeiten zu ermöglichen, bitte das Koordinatensystem nur einmal beschreiben.

Um die geforderten Zuordnungen treffen zu können, müssen Verlauf und charakteristische Werte angegeben sein. Diese sind Schnittpunkte mit den Achsen, Fixpunkte, asymptotisches Verhalten (ohne den Begriff Asymptote zu verwenden), Symmetrie; hilfreich ist die Angabe von Punkten mit ganzzahligen Koordinaten.

Zum leichteren Auffinden sind die Namen der Funktionen an den Anfang der Beschreibung gesetzt.

Layouttabelle: nur visuelle "Tabelle", welche nicht als solche dargestellt wird, da diese einen unnötigen Mehraufwand für den Schüler darstellt.

+++851 |FA 3.1|

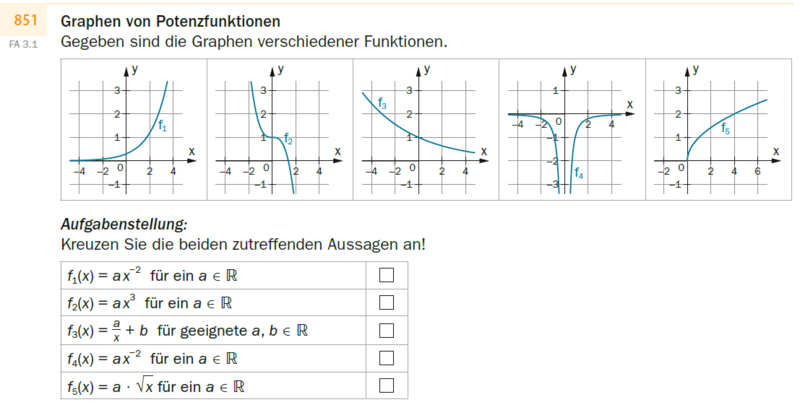
Graphen von Potenzfunktionen

Gegeben sind die Graphen verschiedener Funktionen.

{{Grafik: 5 Koordinatensysteme:

waagrechte Achse: x; [-4; 4], Skalierung: 2;

senkrechte Achse: y; [-1; 3], Skalierung: 1;

---

f_1: Der Graph ist linksgekrümmt steigend. Er beginnt im 2. Quadranten knapp oberhalb der waagrechten Achse langsam steigend, schneidet die senkrechte Achse bei (0|~~0,4), verläuft durch (2|1) und endet stark steigend im 1. Quadraten.

f_2: Der Graph ist fallend, punktsymmetrisch zu (0|1), zuerst links- und dann rechtsgekrümmt. Er beginnt im 2. Quadranten bei ~~(-2|3,2) stark fallend, hat bei (0|1) einen Sattelpunkt, ändert dort sein Krümmungsverhalten, verläuft dann durch den 1. Quadranten und endet fallend im 4. Quadranten.

f_3: Der Graph ist linksgekrümmt fallend. Er beginnt im 2. Quadranten bei ~~(-4,5|3), schneidet die senkrechte Achse bei (0|1) und endet fallend im 1. Quadranten bei ~~(4,5|0,3).

f_4: Der Graph besteht aus 2 Ästen, die symmetrisch zur senkrechten Achse liegen. Der linke Ast liegt im 3. Quadranten. Er ist fallend und rechtsgekrümmt, beginnt knapp unterhalb der waagrechten Achse und endet nahe der senkrechten Achse bei ~~(-0,2|-3,5), Der rechte Ast liegt im 4. Quadranten. Er ist steigend und rechtsgekrümmt, beginnt nahe der senkrechten Achse bei ~~(0,2|-3,5) und endet knapp unterhalb der waagrechten Achse.

f_5: Der Graph liegt im 1. Quadranten, ist rechtsgekrümmt steigend. Er beginnt bei (0|0) und verläuft durch (4|2).}}

---

Aufgabenstellung:

Kreuzen Sie die beiden zutreffenden Aussagen an!

[] f_1(x) =a *x^(-2) für ein a 'el 'R

[] f_2(x) =a *x^3 für ein a 'el 'R

[] f_3(x) =a/x +b für geeignete a, b 'el 'R

[] f_4(x) =a *x^(-2) für ein a 'el 'R

[] f_5(x) =a *'w(x) für ein a 'el 'R

-----