Beispiel 098 - Funktionen und Ableitungen
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS Jänner 2020 Beispiel 16 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
{{Grafik: Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: f_i';
---
Ableitungsfunktionen A - F
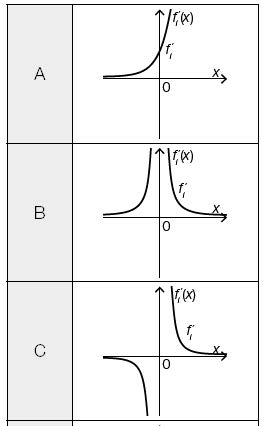
A: Der Graph von f_i' beginnt im 2. Quadranten nahe der x-Achse, ist steigend, linksgekrümmt (positiv gekrümmt) und endet im 1. Quadranten.
---
B: Der Graph von f_i' besteht aus 2 Ästen, die symmetrisch zur senkrechten Achse sind.
Der linke Ast beginnt im 2. Quadranten nahe der x-Achse, ist steigend, linksgekrümmt (positiv gekrümmt) und endet im 2 Quadranten nahe der senkrechten Achse.
Der rechte Ast beginnt im 1. Quadranten nahe der senkrechten Achse, ist fallend, linksgekrümmt (positiv gekrümmt) und endet im 1. Quadranten nahe der x-Achse.
---
C: Der Graph von f_i' besteht aus 2 Ästen, die symmetrisch zum Ursprung sind.
Der linke Ast beginnt im 3. Quadranten nahe der x-Achse, ist fallend, rechtsgekrümmt (negativ gekrümmt) und endet im 3. Quadranten nahe der senkrechten Achse.
Der rechte Ast beginnt im 1. Quadranten nahe der senkrechten Achse, ist fallend, linksgekrümmt (positiv gekrümmt) und endet im 1. Quadranten nahe der waagrechten Achse.
---
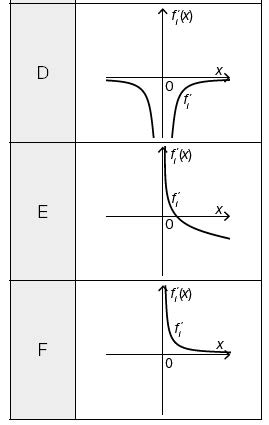
D: Der Graph von f_i' besteht aus 2 Ästen, die symmetrisch zur senkrechten Achse sind.
Der linke Ast beginnt im 3. Quadranten nahe der x-Achse, ist fallend, rechtsgekrümmt (negativ gekrümmt) und endet im 3. Quadranten nahe der senkrechten Achse.
Der rechte Ast beginnt im 4. Quadranten nahe der senkrechten Achse, ist steigend, rechtsgekrümmt (positiv gekrümmt) und endet im 4. Quadranten nahe der waagrechten Achse.
---
E: Der Graph von f_i' beginnt im 1. Quadranten nahe der senkrechten Achse, ist fallend, linksgekrümmt (positiv gekrümmt) und endet im 4. Quadranten.
---
F: Der Graph von f_i' beginnt im 1. Quadranten nahe der senkrechten Achse, ist fallend, linksgekrümmt (positiv gekrümmt) und endet im 1. Quadranten nahe der waagrechten Achse.}}