Beispiel 171 - Halbwertszeit einer Exponentialfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Category:Übungsbeispiele Category:SE1 Category:SE2 Category:Koordinatensystem Category:Ausfüllen Category:Nummerierung/Kennzeichnung v…“) |
|||
| Zeile 35: | Zeile 35: | ||
Die Grafik zeigt, wie sich die Impulsrate im Laufe der Zeit exponentiell ändert. | Die Grafik zeigt, wie sich die Impulsrate im Laufe der Zeit exponentiell ändert. | ||
| − | {{Grafik: | + | {{Grafik: Koordinatensystem: |
| − | |||
| − | Koordinatensystem | ||
waagrechte Achse: Zeit (min); [0; 140]; Skalierung: 10; | waagrechte Achse: Zeit (min); [0; 140]; Skalierung: 10; | ||
Version vom 7. April 2022, 09:12 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 200
Original
Aufbereitet
Neben dem Verlauf müssen Werte angegeben werden, die die Halbwertszeit erkennen lassen. Zu viele Wertepaare sind aber zu vermeiden. Ganzzahlige Wertepaaren sind nach Möglichkeit zu bevorzugen.
+++892. |FA 5.5|
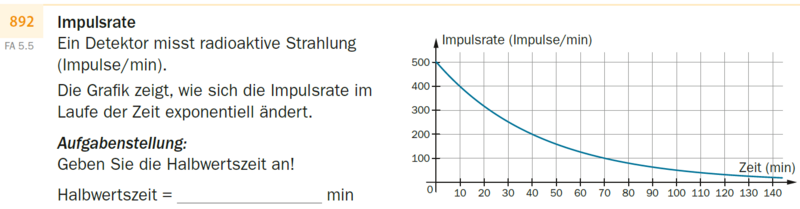
Impulsrate
Ein Detektor misst radioaktive Strahlung (Impulse/min).
Die Grafik zeigt, wie sich die Impulsrate im Laufe der Zeit exponentiell ändert.
{{Grafik: Koordinatensystem:
waagrechte Achse: Zeit (min); [0; 140]; Skalierung: 10;
senkrechte Achse: Impulsrate (Impulse/min); [0; 500]; Skalierung: 100;
---
Der Graph ist linksgekrümmt fallend. Er beginnt bei (0|500), verläuft durch (10|400); (40|200); (70|100) und endet knapp oberhalb der waagrechten Achse bei (140|~~30).}}
---
Aufgabenstellung:
Geben Sie die Halbwertszeit an!
Halbwertszeit =[] min
-----