Beispiel 076 - Gozintograph: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
|||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 29: | Zeile 29: | ||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| + | |||
| + | !!Kosten und Gewinn | ||
+++B-164 Kosten und Gewinn | +++B-164 Kosten und Gewinn | ||
| Zeile 38: | Zeile 40: | ||
--- | --- | ||
| − | <nowiki>{{</nowiki>Beschreibung des Gozinto-Graphen | + | <nowiki>{{</nowiki>Grafik: Beschreibung des Gozinto-Graphen |
--- | --- | ||
| Zeile 58: | Zeile 60: | ||
10 Pfade: | 10 Pfade: | ||
| − | P1: R_1(a)-Z_1(2)-E_1 | + | P1: R_1(a) - Z_1(2) - E_1 |
| − | P2: R_1(a)-Z_1(4)-E_2 | + | P2: R_1(a) - Z_1(4) - E_2 |
| − | P3: R_1(1)-Z_2(1)-E_1 | + | P3: R_1(1) - Z_2(1) - E_1 |
| − | P4: R_1(1)-Z_2(4)-E_2 | + | P4: R_1(1) - Z_2(4) - E_2 |
| − | P5: R_2(c)-Z_2(1)-E_1 | + | P5: R_2(c) - Z_2(1) - E_1 |
| − | P6: R_2(c)-Z_2(4)-E_2 | + | P6: R_2(c) - Z_2(4) - E_2 |
| − | P7: R_2(1)-Z_3(3)-E_1 | + | P7: R_2(1) - Z_3(3) - E_1 |
| − | P8: R_3(2)-Z_3(3)-E_2 | + | P8: R_3(2) - Z_3(3) - E_2 |
| − | P9: R_3(2)-Z_4(1)-E_1 | + | P9: R_3(2) - Z_4(1) - E_1 |
| − | P10: R_3(2)-Z_4(3)-E_2<nowiki>}}</nowiki> | + | P10: R_3(2) - Z_4(3) - E_2<nowiki>}}</nowiki> |
--- | --- | ||
| − | a | + | a) |
Die Matrix RP beschreibt die Mengen an Rohstoffen, die für die Produktion der Endprodukte pro ME jeweils benötigt werden: | Die Matrix RP beschreibt die Mengen an Rohstoffen, die für die Produktion der Endprodukte pro ME jeweils benötigt werden: | ||
| Zeile 104: | Zeile 106: | ||
'''[]''' | '''[]''' | ||
| − | <nowiki> | + | <nowiki>---</nowiki> |
| − | b | + | b) |
Der Materialbestand im Lager beträgt 1460 ME von R_1, 660 ME von R_2 und 1160 ME von R_3. Es wird eine Produktion gestartet, die nach dem obigen Gozinto-Graphen mit der Matrix RP ='mat[3|2]([5;12][1;7][2;12]) abläuft. (Hinweis: a =2 und c =1 sind hier vorgegeben.) | Der Materialbestand im Lager beträgt 1460 ME von R_1, 660 ME von R_2 und 1160 ME von R_3. Es wird eine Produktion gestartet, die nach dem obigen Gozinto-Graphen mit der Matrix RP ='mat[3|2]([5;12][1;7][2;12]) abläuft. (Hinweis: a =2 und c =1 sind hier vorgegeben.) | ||
| Zeile 119: | Zeile 121: | ||
-) Berechnen Sie die entsprechenden Absatzmengen. | -) Berechnen Sie die entsprechenden Absatzmengen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''[]''' | '''[]''' | ||
Aktuelle Version vom 2. Juni 2022, 08:33 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Inhaltstypen
- Formel
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Absatz
- Aus dem Schulbuch
- Beispiel B_164 aus den Übungsbeispielen Angewandte Mathematik srdp.at
- Seite(n)
- -
Original
Aufbereitet
Bei der Beschreibung des Gozinto-Graphen folgt nach der Legende die Anzahl der Pfade und die einzelnen Pfade, die zu den Endprodukten führen. Die dazugehörigen Mengenangaben stehen in runden Klammern.
!!Kosten und Gewinn
+++B-164 Kosten und Gewinn
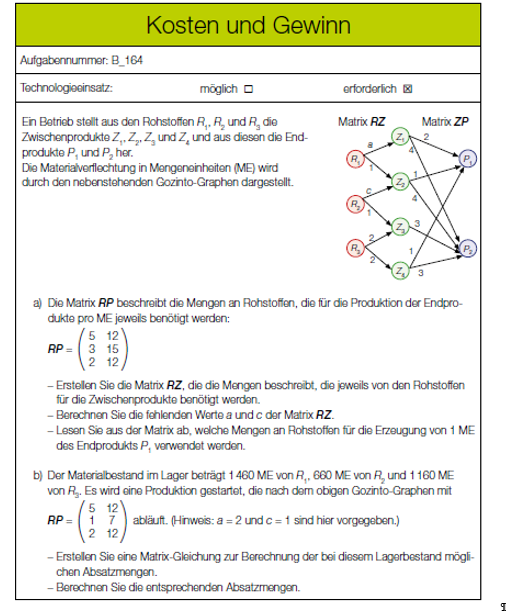
Ein Betrieb stellt aus den Rohstoffen R_1, R_2 und R_3 die Zwischenprodukte Z_1, Z_2, Z_3 und Z_4 und aus diesen die Endprodukte P_1 und P_2 her.
Die Materialverflechtung in Mengeneinheiten (ME) wird durch den nebenstehenden Gozinto-Graphen dargestellt.
---
{{Grafik: Beschreibung des Gozinto-Graphen
---
Legende:
Px ... Pfad x
R_x ... Rohstoff x
Z_x ... Zwischenprodukt x
E_x ... Endprodukt x (P_1; P_2)
---
Matrix RZ | Matrix ZP
10 Pfade:
P1: R_1(a) - Z_1(2) - E_1
P2: R_1(a) - Z_1(4) - E_2
P3: R_1(1) - Z_2(1) - E_1
P4: R_1(1) - Z_2(4) - E_2
P5: R_2(c) - Z_2(1) - E_1
P6: R_2(c) - Z_2(4) - E_2
P7: R_2(1) - Z_3(3) - E_1
P8: R_3(2) - Z_3(3) - E_2
P9: R_3(2) - Z_4(1) - E_1
P10: R_3(2) - Z_4(3) - E_2}}
---
a)
Die Matrix RP beschreibt die Mengen an Rohstoffen, die für die Produktion der Endprodukte pro ME jeweils benötigt werden:
RP ='mat[3|2]([5; 12][3; 15][2; 12])
---
–) Erstellen Sie die Matrix RZ, die die Mengen beschreibt, die jeweils von den Rohstoffen für die Zwischenprodukte benötigt werden.
[]
---
–) Berechnen Sie die fehlenden Werte a und c der Matrix RZ.
[]
---
–) Lesen Sie aus der Matrix ab, welche Mengen an Rohstoffen für die Erzeugung von 1 ME des Endprodukts P_1 verwendet werden.
[]
---
b)
Der Materialbestand im Lager beträgt 1460 ME von R_1, 660 ME von R_2 und 1160 ME von R_3. Es wird eine Produktion gestartet, die nach dem obigen Gozinto-Graphen mit der Matrix RP ='mat[3|2]([5;12][1;7][2;12]) abläuft. (Hinweis: a =2 und c =1 sind hier vorgegeben.)
---
–) Erstellen Sie eine Matrix-Gleichung zur Berechnung der bei diesem Lagerbestand möglichen Absatzmengen.
[]
---
-) Berechnen Sie die entsprechenden Absatzmengen.
[]
-----