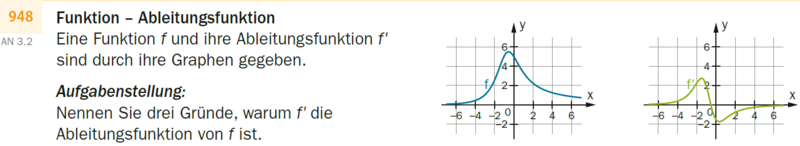Beispiel 173 - Interpretieren - Funktion und 1. Ableitung

Übungstyp und Quelle

Übungstyp

Ausfüllen

Vorhandene Strukturelemente

Nummerierung / Kennzeichnung von Beispielen

Aus dem Schulbuch

195789

Seite(n)

212

Original

Aufbereitet

Achtung:

Bei Zuordnungen zwischen einer Funktion f und seinen Ableitungen müssen bei der Funktion f Wendestellen und Extremstellen angegeben werden;

Bei der 1. Ableitung müssen Extremwerte und Nullstellen angegeben werden.

Bei der 2. Ableitung müssen die Nullstellen angegeben werden.

+++948 |AN 3.2|

Funktion und Ableitungsfunktion

Eine Funktion f und ihre Ableitungsfunktion f' sind durch ihre Graphen gegeben.

{{Grafik: 2 Koordinatensysteme:

waagrechte Achse: x; [-6; 6], Skalierung: 2;

senkrechte Achse: y; [-2; 6], Skalierung: 2;

---

Der dargestellte Graph von f beginnt linksgekrümmt steigend im 2. Quadranten knapp oberhalb der waagrechten Achse, hat ein Maximum (Hochpunkt) im 2. Quadranten und endet fallend und wieder linksgekrümmt im 1. Quadranten. Charakteristische Wertepaare (ungefähre Werte): W_1 =(-1,5|)3); H =(-0,8|5,5); W_2 =(2|2).

---

Der dargestellte Graph von f' beginnt linksgekrümmt steigend im 2. Quadranten knapp oberhalb der waagrechten Achse, hat ein Maximum (Hochpunkt) im 2. Quadranten, ein Minimum (Tiefpunkt) im 4. Quadranten und endet rechtsgekrümmt steigend knapp unterhalb der waagrechten Achse im 4. Quadranten. Charakteristische Wertepaare (ungefähre Werte): H =(-1,5|2,5), N =(-0,8|0); T =(-1|2)}}

---

Aufgabenstellung:

Nennen Sie drei Gründe, warum f' die Ableitungsfunktion von f ist.

[]

-----