Beispiel 163 - Wirtschaftsmathematik; Erlös, Kosten - Zeichnen: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 31: | Zeile 31: | ||
Hinweis: Beim Ablesen der Funktionswerte ist darauf zu achten, dass sich die Gewinnwerte aus der Differenz zwischen Erlös und Kosten ergeben. | Hinweis: Beim Ablesen der Funktionswerte ist darauf zu achten, dass sich die Gewinnwerte aus der Differenz zwischen Erlös und Kosten ergeben. | ||
| − | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family: | + | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> |
+++1071 | +++1071 | ||
Version vom 3. Mai 2022, 15:37 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 241
Original
Aufbereitet
Neben einem möglichst kurz gehaltenen Verlaufsbeschreibungen ist das Anlegen einer Wertetabelle notwendig, um diverse Aufgaben lösen zu können.
Es sind die Funktionswerte aller Graphen an folgenden Stellen anzugeben: Schnittstellen von 2 oder mehr Graphen, Maximalwerte und Nullstellen sowie die Wendestellen einzelner Graphen
Reihenfolge: K(osten); E(rlös); G(ewinn); p(reis)
Hinweis: Beim Ablesen der Funktionswerte ist darauf zu achten, dass sich die Gewinnwerte aus der Differenz zwischen Erlös und Kosten ergeben.
+++1071
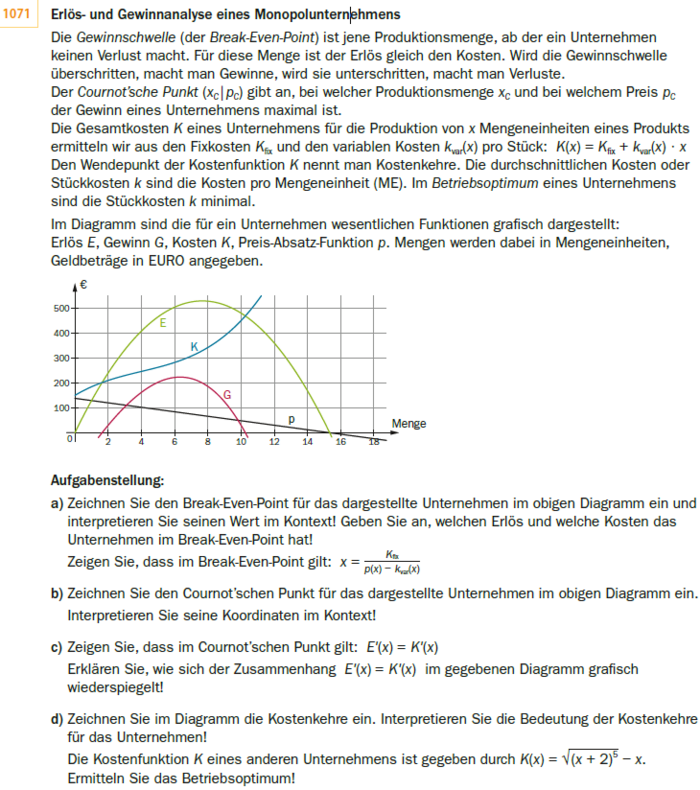
Erlös- und Gewinnanalyse eines Monopolunternehmens
Die Gewinnschwelle (der Break-Even-Point) ist jene Produktionsmenge, ab der ein Unternehmen keinen Verlust macht. Für diese Menge ist der Erlös gleich den Kosten. Wird die Gewinnschwelle überschritten, macht man Gewinne, wird sie unterschritten, macht man Verluste.
Der Cournot'sche Punkt (x_C|p_C) gibt an, bei welcher Produktionsmenge x_C und bei welchem Preis p_C der Gewinn eines Unternehmens maximal ist.
Die Gesamtkosten K eines Unternehmens für die Produktion von x Mengeneinheiten eines Produkts ermitteln wir aus den Fixkosten K_(fix) und den variablen Kosten k_(var)(x) pro Stück: K(x) =K_(fix) +k_(var)(x) *x
Den Wendepunkt der Kostenfunktion K nennt man Kostenkehre. Die durchschnittlichen Kosten oder Stückkosten k sind die Kosten pro Mengeneinheit (ME). Im Betriebsoptimum eines Unternehmens sind die Stückkosten k minimal.
Im Diagramm sind die für ein Unternehmen wesentlichen Funktionen grafisch dargestellt:
Erlös E, Gewinn G, Kosten K, Preis-Absatz-Funktion p. Mengen werden dabei in Mengeneinheiten, Geldbeträge in EURO angegeben.
{{Grafik: Koordinatensystem:
waagrechte Achse: Menge; [0; 18]; Skalierung: 2;
senkrechte Achse: €; [0; 500]; Skalierung: 100;
---
Der dargestellte Graph von K (blau) ist s-förmig gekrümmt. Er steigt rechtsgekrümmt von (0|~~150) bis (6,5|290), steigt linksgekrümmt weiter bis ~~(11|550).
Der dargestellte Graph von E (grün) ist rechtsgekrümmt, steigt von (0|0) bis ~~(7,5|520) und fällt bis (~~15,5|0).
K liegt unterhalb E: zwischen den Schnittstellen bei ~~1,8 und ~~10,5.
Der dargestellte Graph von G (rot) ist rechtsgekrümmt, steigt von (~~1,8|0) bis ~~(6,5|295) und fällt bis (~~10,5|0).
Der dargestellte Graph von p (schwarz) fällt linear von (0|~~150) bis (~~15,5|0)
p liegt unterhalb E: zwischen den Schnittstellen bei ~~1 und ~~15,5.
p liegt unterhalb G: zwischen den Schnittstellen bei ~~3 und ~~9,8.
Die Werte aller Graphen sind an jenen Stellen, die auch Schnittpunkte von mindestens zwei Graphen oder Maximalwerte oder Wendestellen (ungefähre Werte) sind tabellarisch angegeben:
---
Menge | K | E | G | p
0| 150 | 0 | - | 140
1 | 190 | 130 | - | 130
1,8 | 200| 200 | 0 | 120
3 | 240 | 345 | 105 | 105
6,5 | 290| 510 | 220 | 80
7,5 | 330 | 530 |200 | 75
9,8 | 440 | 490 | 50 | 50
10,5 | 460 | 460 | 0 | 45
15,5 | - | 0 |- | 0
---
Aufgabenstellung:
a)
Zeichnen Sie den Break-Even-Point für das dargestellte Unternehmen im obigen Diagramm ein und interpretieren Sie seinen Wert im Kontext! Geben Sie an, welchen Erlös und welche Kosten das Unternehmen im Break-Even-Point hat!
Zeigen Sie, dass im Break-Even-Point gilt: x =(K_(fix))/(p(x) -k_(var)(x))
[]
---
b)
Zeichnen Sie den Cournot'schen Punkt für das dargestellte Unternehmen im obigen Diagramm ein.
Interpretieren Sie seine Koordinaten im Kontext!
[]
---
c)
Zeigen Sie, dass im Cournot'schen Punkt gilt: E'(x) =K'(x)
Erklären Sie, wie sich der Zusammenhang E'(x) =K'(x) im gegebenen Diagramm grafisch widerspiegelt!
[]
---
d)
Zeichnen Sie im Diagramm die Kostenkehre ein. Interpretieren Sie die Bedeutung der Kostenkehre für das Unternehmen!
Die Kostenfunktion K eines anderen Unternehmens ist gegeben durch K(x) ='w((x +2)^5) -x.
Ermitteln Sie das Betriebsoptimum!
[]
-----