Beispiel 093 - Polynomfunktion und bestimmte Integrale

Übungstyp und Quelle

Übungstyp

-

Vorhandene Inhaltstypen

Informationsgrafik

Vorhandene Strukturelemente

-

Aus dem Schulbuch

Matura AHS Jänner 2020 Beispiel 18 (matura.gv.at - Mathematik)

Seite(n)

-

Original

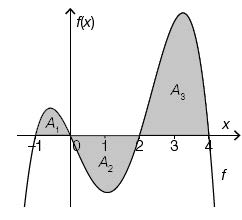
Nachstehend ist der Graph einer Polynomfunktion f mit den Nullstellen x_1 =-1, x_2 =0, x_3 =2 und x_4 =4 dargestellt.

Für die mit A_1, A_2 und A_3 gekennzeichneten Flächeninhalte gilt: A_1 =0,4, A_2 =1,5 und A_3 =3,2. (Abb. 18)

Aufbereitet

Nachstehend ist der Graph einer Polynomfunktion f mit den Nullstellen x_1 =-1, x_2 =0, x_3 =2 und x_4 =4 dargestellt.

Für die mit A_1, A_2 und A_3 gekennzeichneten Flächeninhalte gilt: A_1 =0,4, A_2 =1,5 und A_3 =3,2. (Abb. 18)

{{Grafik: Koordinatensystem:

waagrechte Achse: x; [-2; 5], Skalierung: 1;

senkrechte Achse: f(x); [<>0]; Skalierung: keine;

---

Der Graph beginnt im 3. Quadranten steigend und rechtsgekrümmt (negativ gekrümmt), hat im 2. Quadranten einen Hochpunkt, im 4. Quadranten einen Tiefpunkt, im 1. Quadranten einen weiteren Hochpunkt und endet fallend und wieder rechtsgekrümmt (negativ gekrümmt) im 4. Quadranten.

A_1 =0,4 ist die Fläche zwischen waagrechter Achse und dem Graphen im Intervall [-1; 0] und liegt im 2. Quadranten.

A_2 =1,5 ist die Fläche zwischen waagrechter Achse und dem Graphen im Intervall [0; 2] und liegt im 4. Quadranten.

A_3 =3,2 ist die Fläche zwischen waagrechter Achse und dem Graphen im Intervall [2; 4] und liegt im 4. Quadranten.}}