Beispiel 092 - Polynomfunktionen mit Tangenten
Übungstyp und Quelle
- Übungstyp
- Auswählen
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- Matura AHS Mai 2020 Beispiel 17 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufgabenstellung:
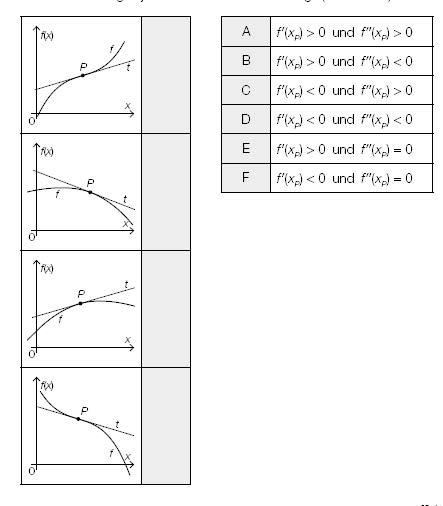
Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu.
Aufbereitet
Layouttabelle: visuelle "Tabelle", welche nicht als solche dargestellt wird, da diese einen unnötigen Mehraufwand für den Schüler darstellt.
+++Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu.
---
A: f'(x_P) >0 und f(x_P) >0
B: f'(x_P) >0 und f(x_P) <0
C: f'(x_P) <0 und f(x_P) >0
D: f'(x_P) <0 und f(x_P) <0
E: f'(x_P) >0 und f(x_P) =0
F: f'(x_P) <0 und f(x_P) =0
---
{{Grafik: Abb. 17_1:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist streng monoton steigend. Bis zum Punkt P ist er rechts gekrümmt und ab dem Punkt P links gekrümmt. Die Tangente t im Punkt P ist streng monoton steigend.}}
---
[] Abb. 17_1
---
{{Grafik: Abb. 17_2:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton fallend.}}
---
[] Abb. 17_2
---
{{Grafik: Abb. 17_3:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton steigend.}}
---
[] Abb. 17_3
---
{{Grafik: Abb. 17_4:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist streng monoton fallend. Bis zum Punkt P verläuft er links gekrümmt und ab dem Punkt P rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton fallend.}}
---
[] Abb. 17_4
-----