Beispiel 168 - Zuordnung - Grade von Polynomfunktionen

Übungstyp und Quelle

Übungstyp

Auswählen

Vorhandene Strukturelemente

Nummerierung / Kennzeichnung von Beispielen

Aus dem Schulbuch

195789

Seite(n)

193

Original

Aufbereitet

Der Begriff Parabel ist bei dieser Beschreibung nicht verwendet, weil damit sofort der Grad bekannt ist.

Um die Orientierung und das schnelle Arbeiten zu ermöglichen, das Koordinatensystem nur einmal beschreiben und bei der Beschreibung die Wahlmöglichkeit an den Zeilenanfang stellen.

Die Tabelle mit den Auswahlmöglichkeiten wie immer vor die Ankreuzungsmöglichkeiten positionieren.

+++861. |FA 4.1|

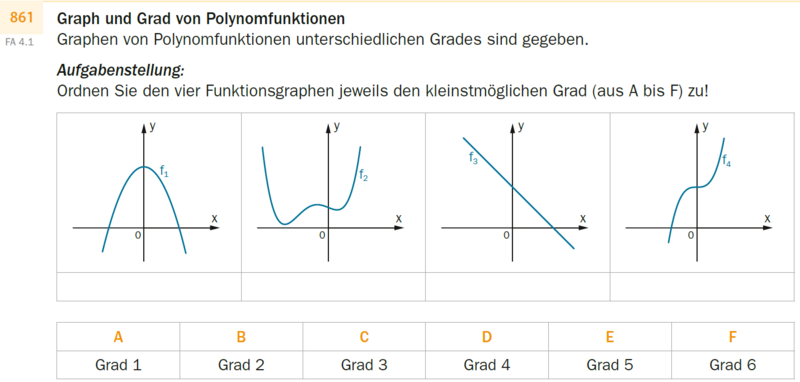
Graph und Grad von Polynomfunktionen

Graphen von Polynomfunktionen unterschiedlichen Grades sind gegeben.

---

Aufgabenstellung:

Ordnen Sie den vier Funktionsgraphen jeweils den kleinstmöglichen Grad (aus A bis F) zu!

{{Grade A bis F}}

A: Grad 1

B: Grad 2

C: Grad 3

D: Grad 4

E: Grad 5

F: Grad 6

---

{{Grafik: 4 Koordinatensysteme ohne Skalierungen:

waagrechte Achse: x;

senkrechte Achse: y;

---

[] der dargestellte Graph von f_1 ist zur senkrechten Achse symmetrisch. Er beginnt fallend im 2. Quadranten, hat ein Minimum (Tiefpunkt) auf der positiven senkrechten Achse und endet steigend im 1. Quadranten.

[] der dargestellte Graph von f_2 beginnt im 2. Quadranten linksgekrümmt fallend bis zu einem lokalen Minimum (Tiefpunkt) im 2. Quadranten, steigt zuerst links- dann rechtsgekrümmt bis zum lokalen Maximum (Hochpunkt) im 2. Quadranten, sinkt zuerst rechts- dann linksgekrümmt bis zu einem lokalen Minimum (Tiefpunkt) im 1. Quadranten und endet steigend und linksgekrümmt im 1. Quadranten

[] der dargestellte Graph von f_3 ist linear fallend. Er beginnt im 2. Quadranten, verläuft dann im 1. und endet im 4. Quadranten.

[] der dargestellte Graph von f_4 ist punktsymmetrisch zu einem Punkt auf der positiven senkrechten Achse. Er beginnt im dritten Quadranten rechtsgekrümmt steigend, verläuft weiter rechtsgekrümmt steigend durch den zweiten Quadranten, ändert das Krümmungsverhalten im Schnittpunkt mit der senkrechten Achse und endet linksgekrümmt steigend im 1. Quadranten.}}

-----