Beispiel 185 - Integral - Zeichnen, Interpretieren
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 244
Original
Aufbereitet
+++1076
Konsumentenrente
Der Preis p(x) (in Euro), den die Konsumenten für ein Produkt zahlen würden, hängt von der produzierten Menge x (in Mengeneinheiten ME) ab. Der tatsächliche Marktpreis p^- (in Euro) ist fix vorgegeben und wird beispielsweise von einem marktbeherrschenden Unternehmen festgelegt.
Wird eine Menge von x^- ME produziert, so gilt p(x^-) =p^-- und der Markt ist im Gleichgewicht. Daher wird x^- Gleichgewichtsmenge genannt. Für Mengen x kleiner als die Gleichgewichtsmenge kann die Differenz p(x) -p^- als Ersparnis der Konsumenten interpretiert werden.
Das bestimmte Integral 'int[0; x^-]((p(x) -p^-) 'dx) gibt die Gesamtsumme aller Ersparnisse auf Konsumentenseite an und wird als Konsumentenrente (engl. consumer's surplus) bezeichnet.
Für ein bestimmtes Produkt seien die Nachfragefunktion p durch p(x) =100 -4 *x^2 und der Marktpreis p^- =64 € gegeben.
---
Aufgabenstellung:
a.)
Berechnen Sie die Gleichgewichtsmenge x^-.
[]
Interpretieren Sie den Monotonieverlauf der Funktion p im gegebenen Kontext.
[]
---
b.)
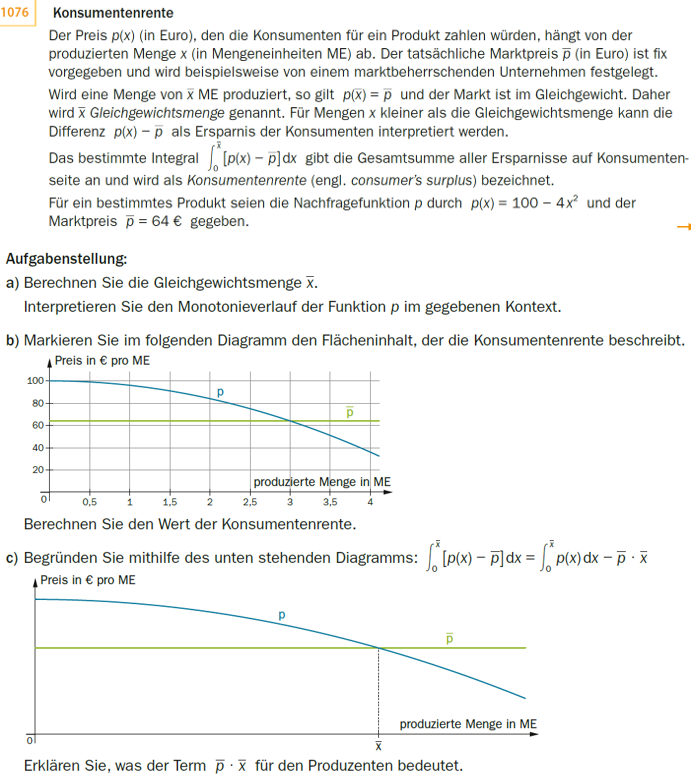
Markieren Sie im folgenden Diagramm den Flächeninhalt, der die Konsumentenrente beschreibt.
{{Grafik:
Koordinatensystem:
waagrechte Achse: produzierte Menge in ME; [0; 4]; Skalierung: 0,5;
senkrechte Achse: Preis in € pro ME; [0; 100]; Skalierung: 20;
---
Der dargestellte Graph von p (blau) ist rechtsgekrümmt. Er fällt von (0|100) bis (4|~~18).
Der dargestellte Graph von p^- (grün) verläuft parallel zur waagrechten Achse von (0|~~62) bis (4|~62).
Der Graph von p^- liegt bis zur Schnittstelle bei (3|~~62) unterhalb des Graphen von p.}}
{{Alternativ: Beschreibung}}: []
---
Berechnen Sie den Wert der Konsumentenrente.
[]
---
c.)
Begründen Sie mithilfe des unten stehenden Diagramms: 'int[0; x^-]((p(x) -p^-) 'dx ='int[0; x^-](p(x) 'dx) -p^- *x^-
{{Grafik:
Koordinatensystem: 1. Quadrant ohne Skalierung
waagrechte Achse: produzierte Menge in ME;
senkrechte Achse: Preis in € pro ME;
---
Der dargestellte Graph von p (blau) ist rechtsgekrümmt fallend ab der positiven senkrechten Achse.
Der dargestellte Graph von p^- (grün) beginnt unterhalb von p (blau) an der positiven senkrechten Achse und verläuft parallel zur waagrechten Achse.
Der Graph von p^- liegt bis zur Schnittstelle an der Stelle x^- unterhalb des Graphen von p.}}
[]
---
Erklären Sie, was der Term p *x für den Produzenten bedeutet.
[]
-----