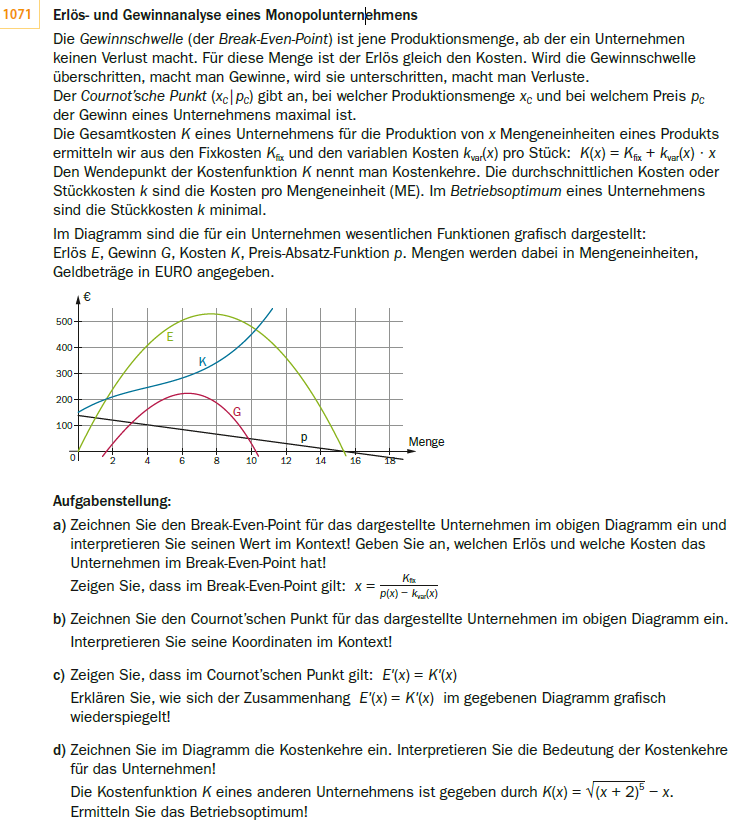
Beispiel 163 - Wirtschaftsmathematik; Erlös, Kosten - Zeichnen
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 184
Original
Aufbereitet
In der Wirtschaftsmathematik ist neben möglichst kurz gehaltenen Verlaufsbeschreibungen oft das Anlegen einer Wertetabelle notwendig, um diverse Aufgaben lösen zu können.
Es sind die Funktionswerte aller Graphen an folgenden Stellen anzugeben: Schnittstellen von 2 oder mehr Graphen, Maximalwerte und Nullstellen sowie die Wendestellen einzelner Graphen.
Reihenfolge: K(osten); E(rlös); G(ewinn); P(reis)
Hinweis: Beim Ablesen der Funktionswerte ist darauf zu achten, dass sich die Gewinnwerte aus der Differenz zwischen Erlös und Kosten ergeben.
Zu viele Punktangaben sind zu vermeiden. Aufgabenstellung in der Regel nach der Beschreibung, wenn nicht gleichzeitig eine Möglichkeit zum Ankreuzen gegeben ist.
+++819. |FA 1.7|
Erlös und Kosten
Die Funktion E beschreibt den Erlös eines Unternehmens (in €) in Abhängigkeit von der Produktionsmenge x. Die Funktion K beschreibt die dabei entstehenden Kosten in €.
{{Grafik:
Koordinatensystem
waagrechte Achse: Produktionsmenge x (in 1000 Stück); [0; 60]; Skalierung: 5;
senkrechte Achse: (K(x), E(x) (in 1000 €); [0; 30]; Skalierung: 5;
---
Der dargestellte Graph von E ist rechtsgekrümmt. Er steigt von (0|0 bis (30|30) und fällt bis (60|0).
Der dargestellte Graph von K ist s-förmig gekrümmt. Er steigt rechtsgekrümmt von (0|20) bis ~(25|27), dann linksgekrümmt bis ~~(60|32).
K liegt unter E: zwischen den Schnittstellen bei ~~17,5 und ~~40.}}
---
Aufgabenstellung:
Kennzeichnen Sie in der nachstehenden Abbildung diejenige Produktionsmenge, bei der das Unternehmen keinen Verlust macht!
{{Alternativ: Beschreibung}}: []
-----