Beispiel 186 - Modellierter Graph /Säulendiagramm: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
==Aufbereitet== | ==Aufbereitet== | ||
| + | |||
| + | Datentabelle: Schulbuch der 12. Schulstufe, daher Word-Tabelle | ||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| Zeile 43: | Zeile 45: | ||
Im Säulendiagramm entspricht jeder 11 Säulen einem Jahr. Die Höhe gibt den Umsatz an. (Darstellung in Tabellenform). Die Fläche der Säulen ist markiert. | Im Säulendiagramm entspricht jeder 11 Säulen einem Jahr. Die Höhe gibt den Umsatz an. (Darstellung in Tabellenform). Die Fläche der Säulen ist markiert. | ||
| − | + | [[Datei:Beispiel 186 - Modellierter Graph Säulendiagramm Word-Tabelle 4.png|650px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Der modellierte Funktionsgraph von R beginnt linksgekrümmt und endet rechtsgekrümmt. Er beginnt bei (1|~~1,5), fällt bis (2|~~2,2), steigt bis (8|~~8,4) und endet bei (11|~~2).}} | Der modellierte Funktionsgraph von R beginnt linksgekrümmt und endet rechtsgekrümmt. Er beginnt bei (1|~~1,5), fällt bis (2|~~2,2), steigt bis (8|~~8,4) und endet bei (11|~~2).}} | ||
Aktuelle Version vom 16. Mai 2024, 09:31 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 244, 245
Original
Aufbereitet
Datentabelle: Schulbuch der 12. Schulstufe, daher Word-Tabelle
+++1077
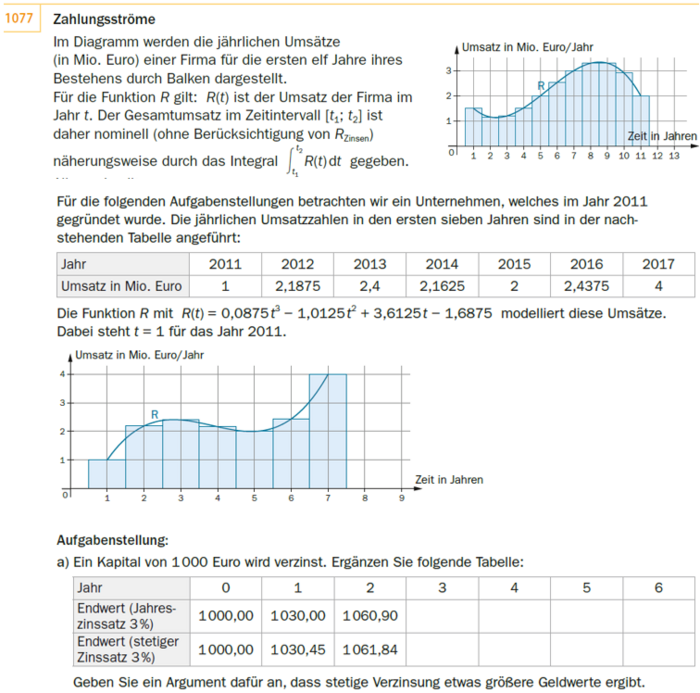
Zahlungsströme
Im Diagramm werden die jährlichen Umsätze (in Mio. Euro) einer Firma für die ersten elf Jahre ihres Bestehens durch Balken dargestellt.
{{Grafik: Koordinatensystem:
waagrechte Achse: Zeit in Jahren; [0; 13], Skalierung: 2;
senkrechte Achse: Umsatz in Mio. Euro/Jahr; [0; 3], Skalierung: 1;
---
Es sind ein Säulendiagramm und eine modellierte Funktion dargestellt.
Im Säulendiagramm entspricht jeder 11 Säulen einem Jahr. Die Höhe gibt den Umsatz an. (Darstellung in Tabellenform). Die Fläche der Säulen ist markiert.
Der modellierte Funktionsgraph von R beginnt linksgekrümmt und endet rechtsgekrümmt. Er beginnt bei (1|~~1,5), fällt bis (2|~~2,2), steigt bis (8|~~8,4) und endet bei (11|~~2).}}
---
Für die Funktion R gilt: R(t) ist der Umsatz der Firma im Jahr t. Der Gesamtumsatz im Zeitintervall [t_1; t_2] ist daher nominell (ohne Berücksichtigung von R_(Zinsen)) näherungsweise durch das Integral 'int[t_1; t_2](R(t) 'dt) gegeben.
---
Für die folgenden Aufgabenstellungen betrachten wir ein Unternehmen, welches im Jahr 2011 gegründet wurde. Die jährlichen Umsatzzahlen in den ersten sieben Jahren sind in der nachstehenden Tabelle angeführt:
Die Funktion R mit R(t) =0,0875 *t^3 -1,0125 *t^2 +3,6125 *t -1,6875 modelliert diese Umsätze.
Dabei steht t =1 für das Jahr 2011.
{{Grafik: Koordinatensystem:
waagrechte Achse: Zeit in Jahren; [0; 9], Skalierung: 2;
senkrechte Achse: Umsatz in Mio. Euro/Jahr; [0; 4], Skalierung: 1;
---
Es sind die modellierte Funktion R und ein Säulendiagramm dargestellt.
Der modellierte Funktionsgraph von R ist zuerst rechtsgekrümmt und dann linksgekrümmt. Er beginnt bei (1|1), steigt bis (3|~~2,4), fällt bis (5|2) und endet bei (7|4))
Im Säulendiagramm entspricht jede der 7 Säulen einem Jahr. Die Höhe gibt den Umsatz an. (Darstellung in Tabellenform.)
---
Aufgabenstellung:
a)
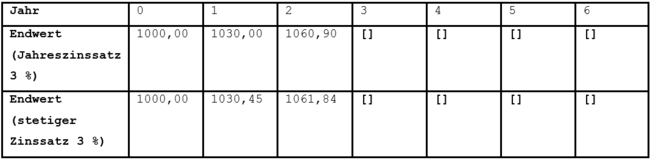
Ein Kapital von 1000 Euro wird verzinst. Ergänzen Sie folgende Tabelle:
Geben Sie ein Argument dafür an, dass stetige Verzinsung etwas größere Geldwerte ergibt.
[]
-----