Beispiel 190 - 2 Säulendiagramme/Wertetabellen vergleichen: Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
==Aufbereitet== | ==Aufbereitet== | ||
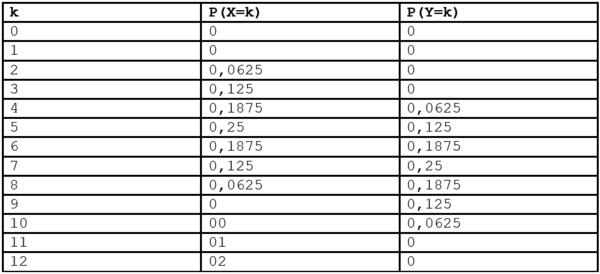
| − | Sollen die Werte von 2 Säulendiagrammen oder 2 Wertetabellen verglichen werden, ist es beim Arbeiten auf der Braillezeile sehr hilfreich, wenn diese in einer dreispaltigen | + | Sollen die Werte von 2 Säulendiagrammen oder 2 Wertetabellen verglichen werden, ist es beim Arbeiten auf der Braillezeile sehr hilfreich, wenn diese in einer dreispaltigen Tabelle dargestellt werden. Voraussetzung sind gleiche Skalierungen auf beiden Achsen. |
Die Ankreuzübung ist im Original als Layouttabelle dargestellt, die besser ohne Tabelle übertragen wird. | Die Ankreuzübung ist im Original als Layouttabelle dargestellt, die besser ohne Tabelle übertragen wird. | ||
Aktuelle Version vom 15. Mai 2024, 08:33 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 234
Original
Aufbereitet
Sollen die Werte von 2 Säulendiagrammen oder 2 Wertetabellen verglichen werden, ist es beim Arbeiten auf der Braillezeile sehr hilfreich, wenn diese in einer dreispaltigen Tabelle dargestellt werden. Voraussetzung sind gleiche Skalierungen auf beiden Achsen.
Die Ankreuzübung ist im Original als Layouttabelle dargestellt, die besser ohne Tabelle übertragen wird.
+++1048 |WS 3.1|
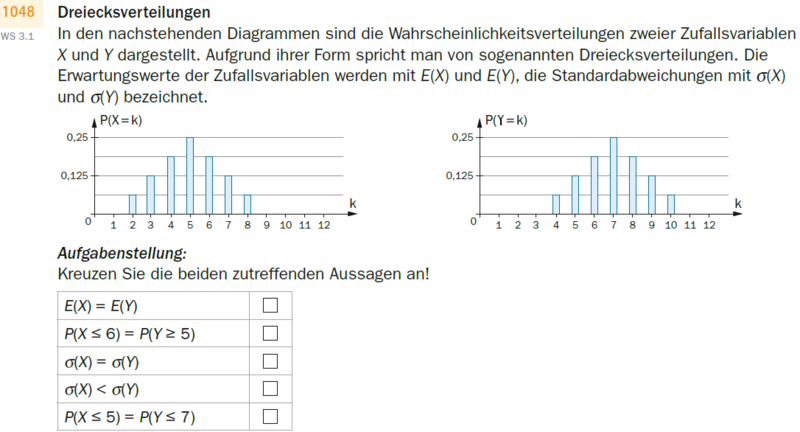
Dreiecksverteilungen
In den nachstehenden Diagrammen sind die Wahrscheinlichkeitsverteilungen zweier Zufallsvariablen X und Y dargestellt. Aufgrund ihrer Form spricht man von sogenannten Dreiecksverteilungen. Die Erwartungswerte der Zufallsvariablen werden mit E(X) und E(Y), die Standardabweichungen mit 'si(X) und 'si(Y) bezeichnet.
{{Grafik: 2 Säulendiagramme P(X=k) und P(Y=k)
}}
---
Aufgabenstellung:
Kreuzen Sie die beiden zutreffenden Aussagen an!
[] E(X) =E(Y)
[] P(X <=6) =P(Y >=5)
[] 'si(X) ='si(Y)
[] 'si(X) <'si(Y)
[] P(X <=5) =P(Y <=7)
-----