Beispiel 085 - Fallende lineare Funktion: Unterschied zwischen den Versionen
| Zeile 20: | Zeile 20: | ||
==Original== | ==Original== | ||
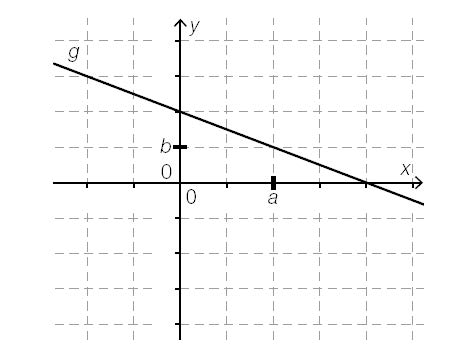
| − | + | Im nachstehend beschriebenen Koordinatensystem (Abb. 5), dessen Achsen unterschiedlich skaliert sind, ist eine Gerade g dargestellt. | |
Auf der x-Achse ist a und auf der y-Achse ist b markiert. Dabei sind a und b ganzzahlig. | Auf der x-Achse ist a und auf der y-Achse ist b markiert. Dabei sind a und b ganzzahlig. | ||
Version vom 27. März 2023, 10:51 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- Matura AHS Mai 2020 Beispiel 5 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Im nachstehend beschriebenen Koordinatensystem (Abb. 5), dessen Achsen unterschiedlich skaliert sind, ist eine Gerade g dargestellt.
Auf der x-Achse ist a und auf der y-Achse ist b markiert. Dabei sind a und b ganzzahlig.
Die Gerade g wird durch y =–2 *x +4 beschrieben.
Aufgabenstellung:
Geben Sie a und b an.
Aufbereitet
+++Im nachstehend beschriebenen Koordinatensystem (Abb. 5), dessen Achsen unterschiedlich skaliert sind, ist eine Gerade g dargestellt. Auf der x-Achse ist a und auf der y-Achse ist b markiert. Dabei sind a und b ganzzahlig. Die Gerade g wird durch y =–2 *x +4 beschrieben.
{{Grafik: Koordinatensystem:
waagrechte Achse: x; Skalierung: a/2;
senkrechte Achse: y; Skalierung: b;
---
Die fallende Gerade g verläuft durch die Punkte (0|2 *b) und (2 *a|0).}}
---
Aufgabenstellung:
Geben Sie a und b an.
a =[]
b =[]
-----