Beispiel 099 - Funktionen und Ableitungen: Unterschied zwischen den Versionen
| Zeile 31: | Zeile 31: | ||
--- | --- | ||
| − | [] Abb. 25_1: | + | '''[]''' Abb. 25_1: |
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | ||
| Zeile 41: | Zeile 41: | ||
--- | --- | ||
| − | [] Abb. 25_2: | + | '''[]''' Abb. 25_2: |
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | ||
| Zeile 51: | Zeile 51: | ||
--- | --- | ||
| − | [] Abb. 25_3: | + | '''[]''' Abb. 25_3: |
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | ||
| Zeile 61: | Zeile 61: | ||
--- | --- | ||
| − | [] Abb. 25_4: | + | '''[]''' Abb. 25_4: |
Graph von s: beginnt im Ursprung, streng monoton steigend und rechtsgekrümmt (negativ gekrümmt) | Graph von s: beginnt im Ursprung, streng monoton steigend und rechtsgekrümmt (negativ gekrümmt) | ||
| Zeile 71: | Zeile 71: | ||
--- | --- | ||
| − | [] Abb. 25_5: | + | '''[]''' Abb. 25_5: |
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt) | ||
| Zeile 81: | Zeile 81: | ||
--- | --- | ||
| − | [] Abb. 25_6: | + | '''[]''' Abb. 25_6: |
Graph von s: beginnt im Ursprung, streng monoton steigend und rechtsgekrümmt (negativ gekrümmt) | Graph von s: beginnt im Ursprung, streng monoton steigend und rechtsgekrümmt (negativ gekrümmt) | ||
Version vom 5. Mai 2022, 07:59 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS September 2019 Beispiel 25 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
Beschreibung der Grafik:
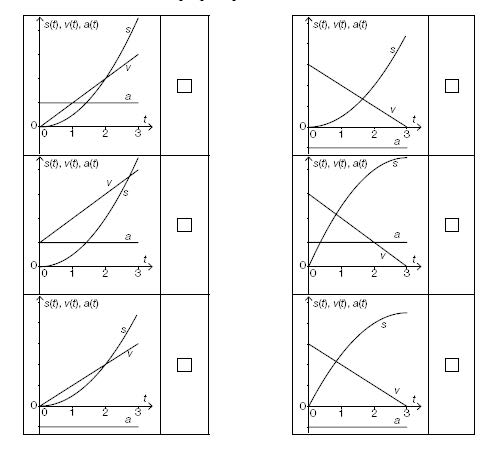
{{Grafik: Abb. 25_1 bis 25_6 und Wahlmöglichkeit:
Koordinatensysteme
waagrechte Achse: t; [0; 3], Skalierung 1
senkrechte Achse: s(t), v(t), a(t); [0; 4], Skalierung 1
---
[] Abb. 25_1:
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt)
Graph von v: streng monoton steigende Gerade durch den Ursprung
Graph von a: eine zur waagrechten Achse parallele Gerade, die im 1. Quadranten verläuft
---
[] Abb. 25_2:
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt)
Graph von v: streng monoton fallende Gerade, deren Darstellung auf der positiven senkrechten Achse beginnt und auf der positiven waagrechten Achse endet
Graph von a: eine zur waagrechten Achse parallele Gerade, die im 4. Quadranten verläuft
---
[] Abb. 25_3:
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt)
Graph von v: streng monoton steigende Gerade, deren Darstellung auf der positiven senkrechten Achse beginnt
Graph von a: eine zur waagrechten Achse parallele Gerade, die im 1. Quadranten verläuft
---
[] Abb. 25_4:
Graph von s: beginnt im Ursprung, streng monoton steigend und rechtsgekrümmt (negativ gekrümmt)
Graph von v: streng monoton fallende Gerade, deren Darstellung auf der positiven senkrechten Achse beginnt und auf der positiven waagrechten Achse endet
Graph von a: eine zur waagrechten Achse parallele Gerade, die im 1. Quadranten verläuft
---
[] Abb. 25_5:
Graph von s: beginnt im Ursprung, streng monoton steigend und linksgekrümmt (positiv gekrümmt)
Graph von v: streng monoton steigende Gerade durch den Ursprung
Graph von a: eine zur waagrechten Achse parallele Gerade, die im 4. Quadranten verläuft
---
[] Abb. 25_6:
Graph von s: beginnt im Ursprung, streng monoton steigend und rechtsgekrümmt (negativ gekrümmt)
Graph von v: streng monoton fallende Gerade, deren Darstellung auf der positiven senkrechten Achse beginnt und auf der positiven waagrechten Achse endet
Graph von a: eine zur waagrechten Achse parallele Gerade, die im 4. Quadranten verläuft}}
---