Beispiel 160 - Eigenschaften einer periodischen Funktion: Unterschied zwischen den Versionen
| Zeile 45: | Zeile 45: | ||
Eine reelle Funktion f ist durch ihren Graphen gegeben. | Eine reelle Funktion f ist durch ihren Graphen gegeben. | ||
| − | {{Grafik: | + | {{Grafik: Koordinatensystem: |
| − | |||
| − | Koordinatensystem | ||
waagrechte Achse: x; [-5; 5]; Skalierung: 1; | waagrechte Achse: x; [-5; 5]; Skalierung: 1; | ||
Version vom 7. April 2022, 09:07 Uhr
Übungstyp und Quelle
- Übungstyp
- Auswählen
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- 195789
- Seite(n)
- 182
Original
Aufbereitet
Angaben bei periodischen Funktionen:
Begriff periodische Funktion;
punktsymmetrisch (zum Ursprung, zu …) oder achsensymmetrisch (zur senkrechten Achse; zu x = …);
verläuft wellenförmig ober- und unterhalb der waagrechten Achse (der Gerade y = …);
Beginn mit steigend/fallend lins-/rechtsgekrümmt und Quadranten;
Anzahl der Perioden;
charakteristische Werte einer Periode (Nullstellen bezogen auf die Mittellinie, Extremwerte);
+++813. |FA 1.5|
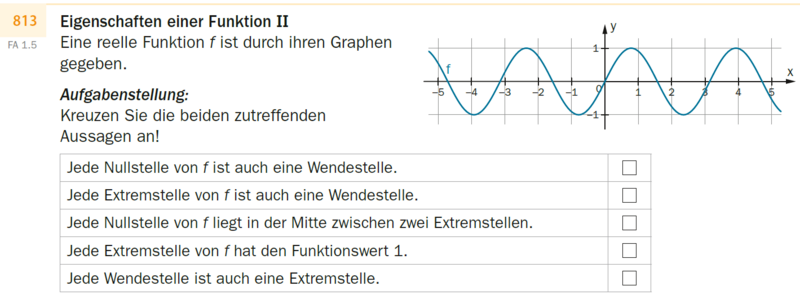
Eigenschaften einer Funktion II
Eine reelle Funktion f ist durch ihren Graphen gegeben.
{{Grafik: Koordinatensystem:
waagrechte Achse: x; [-5; 5]; Skalierung: 1;
senkrechte Achse: y; [-1; 1]; Skalierung: 1;
---
Der dargestellte Graph von f ist periodisch, verläuft wellenförmig oberhalb und unterhalb der waagrechten Achse und ist punktsymmetrisch zum Ursprung. Es sind ~~3 1/2 Perioden dargestellt. Charakteristische Wertepaare einer Periode (Nullstellen, Extremwerte) sind: (0|0); (~~0,8|1); (~~1,6|0); (~~2,4|-1); (~~3,2|0)}}
---
Aufgabenstellung:
Kreuzen Sie die beiden zutreffenden Aussagen an!
[] Jede Nullstelle von f ist auch eine Wendestelle.
[] Jede Extremstelle von f ist auch eine Wendestelle.
[] Jede Nullstelle von f liegt in der Mitte zwischen zwei Extremstellen.
[] Jede Extremstelle von f hat den Funktionswert 1.
[] Jede Wendestelle ist auch eine Extremstelle.
-----