Beispiel 083 - Baumdiagramm 3: Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| − | {{Beschreibung des Baumdiagramms: | + | {{Grafik: Beschreibung des Baumdiagramms: |
Es wird 3 Mal gewürfelt. Es ergeben sich 4 Pfade, die zu einem Sechser führen. | Es wird 3 Mal gewürfelt. Es ergeben sich 4 Pfade, die zu einem Sechser führen. | ||
Version vom 7. April 2022, 07:59 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Aufgabenpool (srdp.at /Stand: 2018): Brettspiele - Teilaufgabe a
- Seite(n)
- -
Original
Beim Würfeln mit einem fairen Spielwürfel treten die Augenzahlen 1 bis 6 jeweils mit gleicher Wahrscheinlichkeit auf.
Bei einem Brettspiel wird zu Beginn des Spiels mit einem fairen Spielwürfel gewürfelt. Um das Spiel beginnen zu können, muss man einen Sechser würfeln. In einem Durchgang hat man maximal 3 Versuche zur Verfügung. Sobald man einen Sechser gewürfelt hat, ist die nächste Spielerin / der nächste Spieler an der Reihe.
Stellen Sie alle möglichen Ausgänge ("Sechser" oder "kein Sechser") für einen Durchgang für eine Spielerin/einen Spieler in einem Baumdiagramm dar.
---
Möglicher Lösungsweg:
Aufbereitet
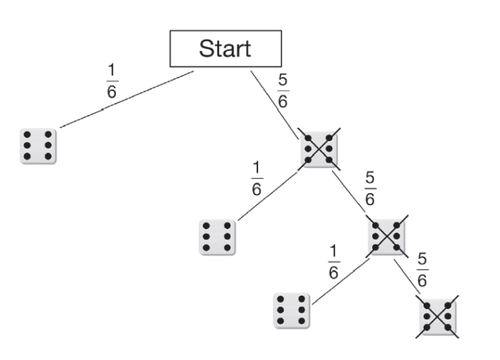
Aufbereitung des Baumdiagramms:
{{Grafik: Beschreibung des Baumdiagramms:
Es wird 3 Mal gewürfelt. Es ergeben sich 4 Pfade, die zu einem Sechser führen.
---
Legende:
s ... Sechser
ks ... kein Sechser
---
1. Pfad: s (1/6)
2. Pfad: ks (5/6) - s (1/6)
3. Pfad: ks (5/6) - ks (5/6) - s (1/6)
4. Pfad: ks (5/6) - ks (5/6) - ks (5/6)}}
-----