Beispiel 106 - Kostenfunktion - Betriebsoptimum: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Category: Übungsbeispiele Category: SE1 Category: SE2 Category: Mathematik ==Übungstyp und Quelle== ;Übungstyp :- ;Vorhandene Inhaltstypen :…“) |
|||
| Zeile 1: | Zeile 1: | ||
[[Category: Übungsbeispiele]] | [[Category: Übungsbeispiele]] | ||
| − | |||
[[Category: SE2]] | [[Category: SE2]] | ||
| − | [[Category: | + | [[Category: Koordinatensystem]] |
| + | |||
==Übungstyp und Quelle== | ==Übungstyp und Quelle== | ||
;Übungstyp | ;Übungstyp | ||
Version vom 20. Mai 2021, 08:43 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura BHS Jänner 2020 Beispiel 7b (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
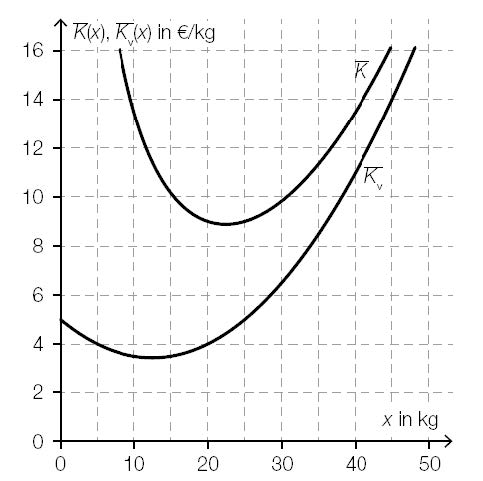
Beschreibung der Grafik:
{{Beschreibung der Abb. 7b:
Koordinatensystem
waagrechte Achse: x in kg; [0; 50], Skalierung: 5;
senkrechte Achse: K^-(x), K^-_v(x) in Euro/kg; [0; 16], Skalierung: 2;
---
Beide Graphen verlaufen in ihrem jeweiligen Darstellungsbereich links gekrümmt.
---
Der Graph von K^-_v (durchgezogene Linie) beginnt ca. im Punkt (0|5) und verläuft bis zum Tiefpunkt bei ca. (12|3,4) streng monoton fallend. Danach verläuft der Graph von K^-_v streng monoton steigend und endet ca. im Punkt (48|16).
---
Der Graph von K^- (punktierte Linie) beginnt ca. im Punkt (8|16) und verläuft bis zum Tiefpunkt bei ca. (22|9) streng monoton fallend. Danach verläuft der Graph von K^- streng monoton steigend und endet ca. im Punkt (45|16).}}