Beispiel 092 - Polynomfunktionen mit Tangenten: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) K (Admin verschob die Seite Beispiel 92 - Polynomfunktionen mit Tangenten nach Beispiel 092 - Polynomfunktionen mit Tangenten) |
|||
| Zeile 2: | Zeile 2: | ||
[[Category: SE1]] | [[Category: SE1]] | ||
[[Category: SE2]] | [[Category: SE2]] | ||
| + | [[Category: Koordinatensystem]] | ||
| + | [[Category: Formel]] | ||
| + | |||
| + | [[Category: Auswählen]] | ||
| + | |||
==Übungstyp und Quelle== | ==Übungstyp und Quelle== | ||
;Übungstyp | ;Übungstyp | ||
| − | : | + | :[[Auswählen]] |
;Vorhandene Inhaltstypen | ;Vorhandene Inhaltstypen | ||
:[[Informationsgrafik]] | :[[Informationsgrafik]] | ||
| Zeile 56: | Zeile 61: | ||
--- | --- | ||
| − | [] Abb. 17_1 | + | '''[]''' Abb. 17_1 |
--- | --- | ||
| Zeile 74: | Zeile 79: | ||
--- | --- | ||
| − | [] Abb. 17_2 | + | '''[]''' Abb. 17_2 |
--- | --- | ||
| Zeile 92: | Zeile 97: | ||
--- | --- | ||
| − | [] Abb. 17_3 | + | '''[]''' Abb. 17_3 |
--- | --- | ||
| Zeile 110: | Zeile 115: | ||
--- | --- | ||
| − | [] Abb. 17_4 | + | '''[]''' Abb. 17_4 |
<nowiki>-----</nowiki> | <nowiki>-----</nowiki> | ||
</div> | </div> | ||
Version vom 19. Mai 2021, 09:15 Uhr
Übungstyp und Quelle
- Übungstyp
- Auswählen
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS Mai 2020 Beispiel 17 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufgabenstellung:
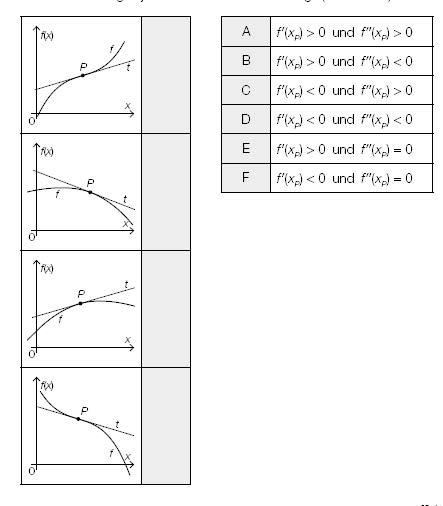
Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu.
Aufbereitet
Aufgabenstellung:
Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu.
---
A: f'(x_P) >0 und f(x_P) >0
B: f'(x_P) >0 und f(x_P) <0
C: f'(x_P) <0 und f(x_P) >0
D: f'(x_P) <0 und f(x_P) <0
E: f'(x_P) >0 und f(x_P) =0
F: f'(x_P) <0 und f(x_P) =0
---
{{Beschreibung der Abb. 17_1:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist streng monoton steigend. Bis zum Punkt P ist er rechts gekrümmt und ab dem Punkt P links gekrümmt. Die Tangente t im Punkt P ist streng monoton steigend.}}
---
[] Abb. 17_1
---
{{Beschreibung der Abb. 17_2:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton fallend.}}
---
[] Abb. 17_2
---
{{Beschreibung der Abb. 17_3:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton steigend.}}
---
[] Abb. 17_3
---
{{Beschreibung der Abb. 17_4:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist streng monoton fallend. Bis zum Punkt P verläuft er links gekrümmt und ab dem Punkt P rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton fallend.}}
---
[] Abb. 17_4
-----