Beispiel 071 - Matrizen

Übungstyp und Quelle

Übungstyp

-

Vorhandene Inhaltstypen

Formel

Vorhandene Strukturelemente

Datentabelle

Überschrift

Seitenzahl

Aus dem Schulbuch

175212

Seite(n)

30

Original

Aufbereitet

Die Überschrift ist zugeordnet, die Seitenangabe steht am Seitenbeginn.

Bei den Tabellen werden Zeilen- und Spalten vertauscht, um die Zeilenlänge 20 zu unterschreiten und beide Tabellen werden gleichzeitig mit einer Legende angekündigt, weil beide Tabellen die gleichen Überschriften haben und dadurch auch die erste Zeile übersichtlich bleibt (unter 20 Zeichen). Die Anzahl der einfachen Bindestriche in der ersten Zeile/ersten Spalte richtet sich nach der längsten Zeilenüberschrift (daher --)

Eine Matrix mit m Zeilen und n Spalten wird durch 'mat[m|n] angekündigt.

Die Matrix selbst steht in runden Klammern, jede Zeile steht innerhalb eckiger Klammern. Zwischen den eckigen Klammern ist kein Abstand, jeder Eintrag wird vom nächsten durch einen Strichpunkt getrennt. Am Ende einer Matrix erfolgt ein "Enter".

z.B:

'mat[3|2]([1; 2][4; 5][6; 7])

'mat[3|1]([1][4][6])

'mat[1|3]([1; 2; 3])

Wird optisch gearbeitet und/oder eine zeilenweise Strukturierung gewünscht, kann dies beim Erlesen sofort durch das Drücken der Eingabetaste erreicht werden.

---

Mit 'det[A] wird nach der Determinante einer Matrix A gefragt.

---

Vorlage für häufig vorkommende Matrizen

'mat[3|1]([][][])

'mat[1|3]([;;])

'mat[2|2]([;][;])

'mat[2|3]([;;][;;])

'mat[3|3]([;;][;;][;;])

'mat[6|6] ([;;;;;][;;;;;][;;;;;][;;;;;][;;;;;][;;;;;])

---

j-30

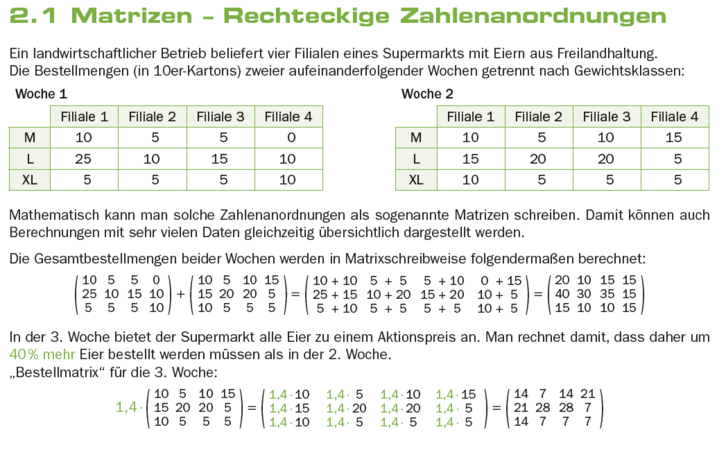
!!2.1 Matrizen - Rechteckige Zahlenanordnungen

Ein landwirtschaftlicher Betrieb beliefert vier Filialen eines Supermarkts mit Eiern aus Freilandhaltung. Die Bestellmengen (in 10er-Kartons) zweier aufeinanderfolgender Wochen getrennt nach Gewichtsklassen:

{{Die beiden Tabellen sind aufgelöst}}

---

Legende:

F1 ... Filiale 1

F2 ... Filiale 2

F3 ... Filiale 3

F4 ... Filiale 4

---

Woche 1:

-- | M | L | XL

F1 | 10 | 25 | 5

F2 | 5 | 10 | 5

F3 | 5 | 15 | 15

F4 | 0 | 10 | 10

---

Woche 2:

-- | M | L | XL

F1 | 10 | 15 | 10

F2 | 5 | 20 | 5

F3 | 10 | 20 | 15

F4 | 15 | 5 | 5

---

Mathematisch kann man solche Zahlenanordnungen als sogenannte Matrizen schreiben. Damit können auch Berechnungen mit sehr vielen Daten gleichzeitig übersichtlich dargestellt werden.

Die Gesamtbestellmengen beider Wochen werden in Matrixschreibweise folgendermaßen berechnet:

'mat[3|4]([10; 5; 5; 0][25; 10; 15; 10][5; 5; 5; 10])

+'mat[3|4]([10; 5; 10; 15][15; 20; 20; 5][10; 5; 5; 5])

='mat[3|4]([10 +10; 5 +5; 5 +10; 0 +15][25 +15; 10 +20; 15 +20; 10 +5][5 +10; 5 +5; 5 +5; 10 +5])

='mat[3|4]([20; 10; 15; 15][40; 30; 35; 15][15; 10; 10; 15])

In der 3. Woche bietet der Supermarkt alle Eier zu einem Aktionspreis an. Man rechnet damit, dass daher um 40 % mehr Eier bestellt werden müssen als in der 2. Woche.

"Bestellmatrix" für die 3. Woche:

1,4 *'mat[3|4]([10; 5; 10; 15][15; 20; 20; 5][10; 5; 5; 5])

='mat[3|4]([1,4 *10; 1,4 *5; 1,4 *10; 1,4 *15][1,4 *15; 1,4 *20; 1,4 *20; 1,4 *5][1,4 *10; 1,4 *5; 1,4 *5; 1,4 *5]) ='mat[3|4]([14; 7; 14; 21][21; 28; 28; 7][14; 7; 7; 7])

-----