Beispiel 090 - Parabel, Polynomfunktion: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Category: Übungsbeispiele Category: SE1 Category: SE2 ==Übungstyp und Quelle== ;Übungstyp :- ;Vorhandene Inhaltstypen :Informationsgrafik ;V…“) |
Admin (Diskussion | Beiträge) |
||
| Zeile 28: | Zeile 28: | ||
--- | --- | ||
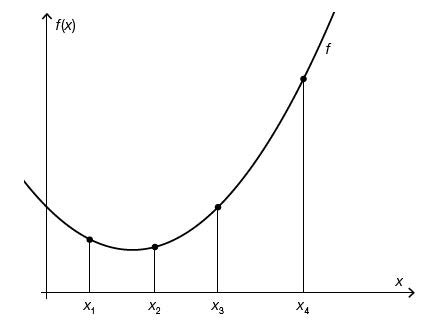
| − | Die nach oben offene Parabel beginnt fallend im | + | Die nach oben offene Parabel beginnt fallend im 2. Quadranten, hat einen Tiefpunkt im 1. Quadranten und endet steigend im 1 Quadranten. Sie fällt an der Stelle x_1, hat zwischen x_1 und x_2 den Tiefpunkt, steigt anfangs weniger dann mehr. Es gilt: |
Ungefähre Angaben der Funktionswerte, wenn der Tiefpunkt mit dem Funktionswert 1 angenommen werden würde: (x_1|1,2), T =(x_T|1), (x_2|1,1); (x_3|2), (x_4|4)}} | Ungefähre Angaben der Funktionswerte, wenn der Tiefpunkt mit dem Funktionswert 1 angenommen werden würde: (x_1|1,2), T =(x_T|1), (x_2|1,1); (x_3|2), (x_4|4)}} | ||
Version vom 9. Februar 2021, 11:27 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS Jänner 2020 Beispiel 13 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
{{Beschreibung der Abb. 13:
Koordinatensystem
waagrechte Achse: x; im 1. Quadranten: x_1 <x_2 <x_3 <x_4
senkrechte Achse: f(x)
---
Die nach oben offene Parabel beginnt fallend im 2. Quadranten, hat einen Tiefpunkt im 1. Quadranten und endet steigend im 1 Quadranten. Sie fällt an der Stelle x_1, hat zwischen x_1 und x_2 den Tiefpunkt, steigt anfangs weniger dann mehr. Es gilt:
Ungefähre Angaben der Funktionswerte, wenn der Tiefpunkt mit dem Funktionswert 1 angenommen werden würde: (x_1|1,2), T =(x_T|1), (x_2|1,1); (x_3|2), (x_4|4)}}
---