Funktionsgrafik ohne Koordinaten: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Category: Bestpractice Category: SE1 Category: SE2 Category: Mathematik Zur Lösung der Aufgabe müssen die Funktionsverläufe beschrieben werd…“) |
|||
| (2 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
:175212 | :175212 | ||
;Seite(n) | ;Seite(n) | ||
| − | : | + | :59 |
==Original== | ==Original== | ||
| Zeile 48: | Zeile 48: | ||
1. Der Graph beginnt nahe der positiven senkrechten Achse, ist fallend und linksgekrümmt und nähert sich der waagrechten Achse. | 1. Der Graph beginnt nahe der positiven senkrechten Achse, ist fallend und linksgekrümmt und nähert sich der waagrechten Achse. | ||
| − | [] | + | '''[]''' |
--- | --- | ||
| − | 2. Der Graph | + | 2. Der Graph beginnt an der senkrechten positiven Achse und ist linear steigend. |
| − | [] | + | '''[]''' |
--- | --- | ||
| Zeile 60: | Zeile 60: | ||
3. Der Graph beginnt nahe der positiven senkrechten Achse, ist streng monoton steigend und rechtsgekrümmt. | 3. Der Graph beginnt nahe der positiven senkrechten Achse, ist streng monoton steigend und rechtsgekrümmt. | ||
| − | [] | + | '''[]''' |
--- | --- | ||
| Zeile 66: | Zeile 66: | ||
4. Der Graph beginnt nahe der positiven senkrechten Achse, ist streng monoton steigend und linksgekrümmt. | 4. Der Graph beginnt nahe der positiven senkrechten Achse, ist streng monoton steigend und linksgekrümmt. | ||
| − | [] | + | '''[]''' |
| − | <nowiki>----- | + | <nowiki>}}</nowiki> |
| + | |||
| + | <nowiki>-----</nowiki> | ||
</div> | </div> | ||
Aktuelle Version vom 13. Februar 2023, 10:41 Uhr
Zur Lösung der Aufgabe müssen die Funktionsverläufe beschrieben werden.
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- 175212
- Seite(n)
- 59
Original
Aufbereitet
In Doppelt geschwungenen Klammern wird ein Lösungsbeispiel vorgegeben. Danach folgen die Anweisungen:
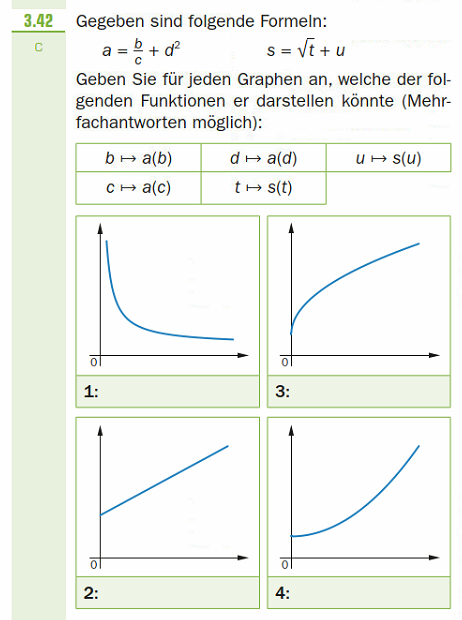
+++3.42 Gegeben sind folgende Formeln:
a =b/c +d^2
s ='w(t) +u
Geben Sie für jeden Graphen an, welche der folgenden Funktionen er dastellen könnte (Mehrfachantworten möglich):
b --> a(b)
d --> a(d)
c --> a(c)
u --> s(u)
t --> s(t)
---
{{Beschreibung der Abb. 3.42 1 -4 und Wahlmöglichkeit
Koordinatensysteme im 1. Quadranten
1. Der Graph beginnt nahe der positiven senkrechten Achse, ist fallend und linksgekrümmt und nähert sich der waagrechten Achse.
[]
---
2. Der Graph beginnt an der senkrechten positiven Achse und ist linear steigend.
[]
---
3. Der Graph beginnt nahe der positiven senkrechten Achse, ist streng monoton steigend und rechtsgekrümmt.
[]
---
4. Der Graph beginnt nahe der positiven senkrechten Achse, ist streng monoton steigend und linksgekrümmt.
[]
}}
-----