Beispiel 092 - Polynomfunktionen mit Tangenten: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[Category: Auswählen]] | [[Category: Auswählen]] | ||
| + | [[Category: Nummerierung/Kennzeichnung von Beispielen]] | ||
==Übungstyp und Quelle== | ==Übungstyp und Quelle== | ||
| Zeile 13: | Zeile 14: | ||
:[[Informationsgrafik]] | :[[Informationsgrafik]] | ||
;Vorhandene Strukturelemente | ;Vorhandene Strukturelemente | ||
| − | : | + | :[[Nummerierung / Kennzeichnung von Beispielen]] |
;Aus dem Schulbuch | ;Aus dem Schulbuch | ||
:Matura AHS Mai 2020 Beispiel 17 ([https://www.matura.gv.at/downloads?tx_solr%5Bfilter%5D%5B0%5D=accessebility%3A1&tx_solr%5Bfilter%5D%5B1%5D=subject%3A%2FMathematik%2F matura.gv.at - Mathematik]) | :Matura AHS Mai 2020 Beispiel 17 ([https://www.matura.gv.at/downloads?tx_solr%5Bfilter%5D%5B0%5D=accessebility%3A1&tx_solr%5Bfilter%5D%5B1%5D=subject%3A%2FMathematik%2F matura.gv.at - Mathematik]) | ||
| Zeile 26: | Zeile 27: | ||
[[Datei:Beispiel 92 - polynomfunktionen mit tangenten.jpg]] | [[Datei:Beispiel 92 - polynomfunktionen mit tangenten.jpg]] | ||
==Aufbereitet== | ==Aufbereitet== | ||
| + | |||
| + | Layouttabelle: nur visuelle "Tabelle", welche nicht als solche dargestellt wird, da diese einen unnötigen Mehraufwand für den Schüler darstellt. | ||
| + | |||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| − | + | +++Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu. | |
| − | |||
| − | Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu. | ||
--- | --- | ||
| Zeile 47: | Zeile 49: | ||
--- | --- | ||
| − | {{ | + | {{Grafik: Abb. 17_1: |
Koordinatensystem | Koordinatensystem | ||
| Zeile 65: | Zeile 67: | ||
--- | --- | ||
| − | {{ | + | {{Grafik: Abb. 17_2: |
Koordinatensystem | Koordinatensystem | ||
| Zeile 83: | Zeile 85: | ||
--- | --- | ||
| − | {{ | + | {{Grafik: Abb. 17_3: |
Koordinatensystem | Koordinatensystem | ||
| Zeile 101: | Zeile 103: | ||
--- | --- | ||
| − | {{ | + | {{Grafik: Abb. 17_4: |
Koordinatensystem | Koordinatensystem | ||
Aktuelle Version vom 15. Mai 2024, 07:55 Uhr
Übungstyp und Quelle
- Übungstyp
- Auswählen
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- Nummerierung / Kennzeichnung von Beispielen
- Aus dem Schulbuch
- Matura AHS Mai 2020 Beispiel 17 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufgabenstellung:
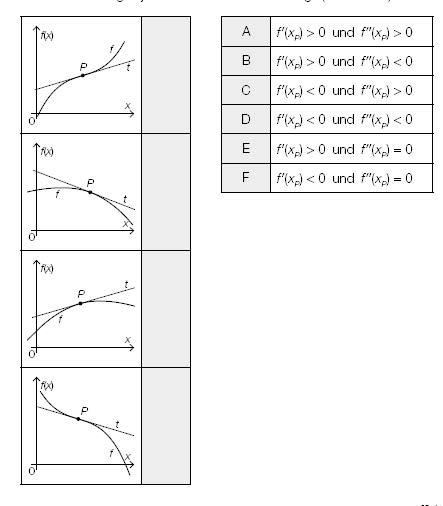
Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu.
Aufbereitet
Layouttabelle: nur visuelle "Tabelle", welche nicht als solche dargestellt wird, da diese einen unnötigen Mehraufwand für den Schüler darstellt.
+++Ordnen Sie den vier Abbildungen jeweils die zutreffende Aussage (aus A bis F) zu.
---
A: f'(x_P) >0 und f(x_P) >0
B: f'(x_P) >0 und f(x_P) <0
C: f'(x_P) <0 und f(x_P) >0
D: f'(x_P) <0 und f(x_P) <0
E: f'(x_P) >0 und f(x_P) =0
F: f'(x_P) <0 und f(x_P) =0
---
{{Grafik: Abb. 17_1:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist streng monoton steigend. Bis zum Punkt P ist er rechts gekrümmt und ab dem Punkt P links gekrümmt. Die Tangente t im Punkt P ist streng monoton steigend.}}
---
[] Abb. 17_1
---
{{Grafik: Abb. 17_2:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton fallend.}}
---
[] Abb. 17_2
---
{{Grafik: Abb. 17_3:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton steigend.}}
---
[] Abb. 17_3
---
{{Grafik: Abb. 17_4:
Koordinatensystem
waagrechte Achse: x;
senkrechte Achse: y;
---
Der Graph von f ist im ersten Quadranten dargestellt und ist streng monoton fallend. Bis zum Punkt P verläuft er links gekrümmt und ab dem Punkt P rechts gekrümmt. Die Tangente t im Punkt P ist streng monoton fallend.}}
---
[] Abb. 17_4
-----