Beispiel 091 - Zwei Parabeln: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
==Aufbereitet== | ==Aufbereitet== | ||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| − | {{ | + | {{Grafik: |
| − | Koordinatensystem | + | Legende: |
| + | |||
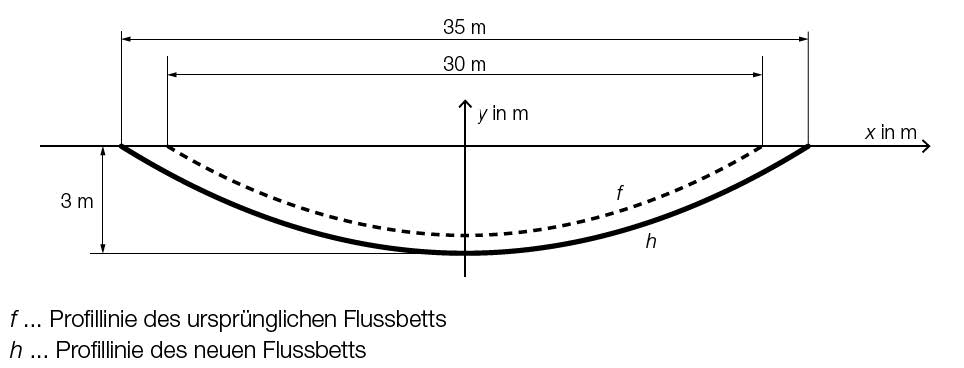
| + | f ... Profillinie des ursprünglichen Flussbetts | ||
| + | |||
| + | h ... Profillinie des neuen Flussbetts | ||
| + | |||
| + | --- | ||
| + | |||
| + | Koordinatensystem: | ||
waagrechte Achse: x in m; [-17,5; 17,5], Skalierung: keine; | waagrechte Achse: x in m; [-17,5; 17,5], Skalierung: keine; | ||
| Zeile 34: | Zeile 42: | ||
Der Scheitelpunkt von f liegt knapp über dem Scheitelpunkt von h. Die Nullstellen von f sind bei -15 und 15.}} | Der Scheitelpunkt von f liegt knapp über dem Scheitelpunkt von h. Die Nullstellen von f sind bei -15 und 15.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
--- | --- | ||
</div> | </div> | ||
Aktuelle Version vom 27. März 2023, 11:30 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura BHS Mai 2018 Beispiel 6c (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
{{Grafik:
Legende:
f ... Profillinie des ursprünglichen Flussbetts
h ... Profillinie des neuen Flussbetts
---
Koordinatensystem:
waagrechte Achse: x in m; [-17,5; 17,5], Skalierung: keine;
senkrechte Achse: y in m; [-3; 0], Skalierung: keine;
---
Die Graphen der Funktionen f und h sind nach oben offene Parabeln.
Der Scheitelpunkt von h ist (0|-3). Die Nullstellen von h sind bei -17,5 und 17,5.
Der Scheitelpunkt von f liegt knapp über dem Scheitelpunkt von h. Die Nullstellen von f sind bei -15 und 15.}}
---