Beispiel 099 - Funktionen und Ableitungen: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
|||
| Zeile 33: | Zeile 33: | ||
'''[]''' Abb. 25_1: | '''[]''' Abb. 25_1: | ||
| − | Graph von s: | + | Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung |
| − | Graph von v: | + | Graph von v: linear steigend, beginnt im Ursprung |
| − | Graph von a: | + | Graph von a: parallel zur waagrechten Achse, verläuft im 1. Quadranten |
--- | --- | ||
| Zeile 43: | Zeile 43: | ||
'''[]''' Abb. 25_2: | '''[]''' Abb. 25_2: | ||
| − | Graph von s: | + | Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung |
| − | Graph von v: | + | Graph von v: linear fallend, beginnt auf der positiven senkrechten Achse und endet auf der positiven waagrechten Achse |
| − | Graph von a: | + | Graph von a: parallel zur waagrechten Achse, verläuft im 4. Quadranten |
--- | --- | ||
| Zeile 53: | Zeile 53: | ||
'''[]''' Abb. 25_3: | '''[]''' Abb. 25_3: | ||
| − | Graph von s: | + | Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung |
| − | Graph von v: | + | Graph von v: linear steigend, beginnt auf der positiven senkrechten Achse |
| − | Graph von a: | + | Graph von a: parallel zur waagrechten Achse, verläuft im 1. Quadranten |
--- | --- | ||
| Zeile 63: | Zeile 63: | ||
'''[]''' Abb. 25_4: | '''[]''' Abb. 25_4: | ||
| − | Graph von s: | + | Graph von s: streng monoton steigend und rechtsgekrümmt (negativ gekrümmt), beginnt im Ursprung |
| − | Graph von v: | + | Graph von v: linear fallend, beginnt auf der positiven senkrechten Achse und endet auf der positiven waagrechten Achse |
| − | Graph von a: | + | Graph von a: parallel zur waagrechten Achse, verläuft im 1. Quadranten |
--- | --- | ||
| Zeile 73: | Zeile 73: | ||
'''[]''' Abb. 25_5: | '''[]''' Abb. 25_5: | ||
| − | Graph von s: | + | Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung |
| − | Graph von v: | + | Graph von v: linear steigend, beginnt im Ursprung |
| − | Graph von a: | + | Graph von a: parallel zur waagrechten Achse, verläuft im 4. Quadranten |
--- | --- | ||
| Zeile 83: | Zeile 83: | ||
'''[]''' Abb. 25_6: | '''[]''' Abb. 25_6: | ||
| − | Graph von s: | + | Graph von s: streng monoton steigend und rechtsgekrümmt (negativ gekrümmt), beginnt im Ursprung |
| − | Graph von v: | + | Graph von v: linear fallend, beginnt auf der positiven senkrechten Achse und endet auf der positiven waagrechten Achse |
| − | Graph von a: | + | Graph von a: parallel zur waagrechten Achse, verläuft im 4. Quadranten}} |
| + | |||
| + | --- | ||
</div> | </div> | ||
Aktuelle Version vom 13. Februar 2023, 11:19 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS September 2019 Beispiel 25 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
Beschreibung der Grafik:
{{Grafik: Abb. 25_1 bis 25_6 und Wahlmöglichkeit:
Koordinatensysteme
waagrechte Achse: t; [0; 3], Skalierung 1;
senkrechte Achse: s(t), v(t), a(t); [0; 4], Skalierung 1;
---
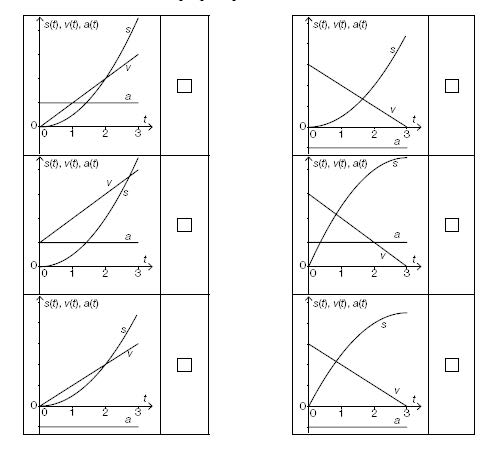
[] Abb. 25_1:
Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung
Graph von v: linear steigend, beginnt im Ursprung
Graph von a: parallel zur waagrechten Achse, verläuft im 1. Quadranten
---
[] Abb. 25_2:
Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung
Graph von v: linear fallend, beginnt auf der positiven senkrechten Achse und endet auf der positiven waagrechten Achse
Graph von a: parallel zur waagrechten Achse, verläuft im 4. Quadranten
---
[] Abb. 25_3:
Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung
Graph von v: linear steigend, beginnt auf der positiven senkrechten Achse
Graph von a: parallel zur waagrechten Achse, verläuft im 1. Quadranten
---
[] Abb. 25_4:
Graph von s: streng monoton steigend und rechtsgekrümmt (negativ gekrümmt), beginnt im Ursprung
Graph von v: linear fallend, beginnt auf der positiven senkrechten Achse und endet auf der positiven waagrechten Achse
Graph von a: parallel zur waagrechten Achse, verläuft im 1. Quadranten
---
[] Abb. 25_5:
Graph von s: streng monoton steigend und linksgekrümmt (positiv gekrümmt), beginnt im Ursprung
Graph von v: linear steigend, beginnt im Ursprung
Graph von a: parallel zur waagrechten Achse, verläuft im 4. Quadranten
---
[] Abb. 25_6:
Graph von s: streng monoton steigend und rechtsgekrümmt (negativ gekrümmt), beginnt im Ursprung
Graph von v: linear fallend, beginnt auf der positiven senkrechten Achse und endet auf der positiven waagrechten Achse
Graph von a: parallel zur waagrechten Achse, verläuft im 4. Quadranten}}
---