Beispiel 102 - Sinusfunktion: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Category: Übungsbeispiele Category: SE1 Category: SE2 Category: Mathematik ==Übungstyp und Quelle== ;Übungstyp :- ;Vorhandene Inhaltstypen :…“) |
|||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category: Übungsbeispiele]] | [[Category: Übungsbeispiele]] | ||
| − | |||
[[Category: SE2]] | [[Category: SE2]] | ||
| − | [[Category: | + | [[Category: Koordinatensystem]] |
| + | |||
==Übungstyp und Quelle== | ==Übungstyp und Quelle== | ||
;Übungstyp | ;Übungstyp | ||
| Zeile 29: | Zeile 29: | ||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| − | {{ | + | {{Grafik: Koordinatensystem quadratisches Koordinatengitter: |
| − | |||
| − | Koordinatensystem quadratisches Koordinatengitter | ||
| − | waagrechte Achse: x | + | waagrechte Achse: x; [-6; 10], Skalierung: 1; |
| − | senkrechte Achse: f(x) | + | senkrechte Achse: f(x); [-3; 4], Skalierung: 1; |
--- | --- | ||
Aktuelle Version vom 8. Juni 2022, 08:52 Uhr
Übungstyp und Quelle
- Übungstyp
- -
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS Jänner 2020 Beispiel 12 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
Aufbereitet
Die folgenden Abkürzungen werden verwendet:
N ... Nullstelle
H ... Hochpunkt
T ... Tiefpunkt
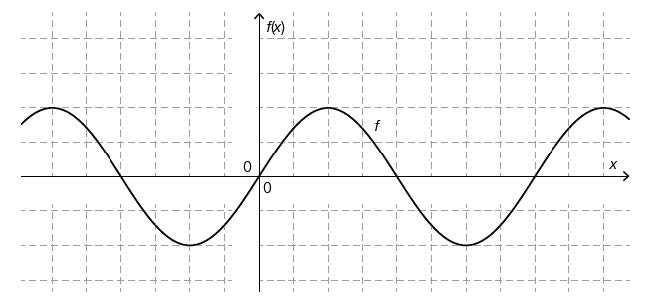
Beschreibung der Grafik:
{{Grafik: Koordinatensystem quadratisches Koordinatengitter:
waagrechte Achse: x; [-6; 10], Skalierung: 1;
senkrechte Achse: f(x); [-3; 4], Skalierung: 1;
---
Der dargestellte Graph der Sinusfunktion ist symmetrisch zur waagrechten Achse und punktsymmetrisch zum Ursprung. Einige charakteristische Wertepaare (in Einheiten): N_1 =(0|0); H =(2|2); N_2 =(4|0), T =(6|-2), N_3 =(8|0).}}
---