Beispiel 095 - Polynomfunktion - Verlaufsbeschreibung

Übungstyp und Quelle

Übungstyp

Ausfüllen

Vorhandene Inhaltstypen

Informationsgrafik

Vorhandene Strukturelemente

-

Aus dem Schulbuch

Matura AHS Mai 2019 für Wiederholer Beispiel 19 (matura.gv.at - Mathematik)

Seite(n)

-

Original

Es gibt Polynomfunktionen vierten Grades, die genau drei Nullstellen x_1, x_2 und x_3 mit x_1, x_2, x_3 'el 'R und x_1 <x_2 <x_3 haben.

Aufgabenstellung:

Skizzieren Sie im nachstehenden Koordinatensystem im Intervall [-4; 4] den Verlauf des Graphen einer solchen Funktion f mit allen drei Nullstellen im Intervall [-3; 3]! (Abb. 10)

Aufbereitet

Es gibt Polynomfunktionen vierten Grades, die genau drei Nullstellen x_1, x_2 und x_3 mit x_1, x_2, x_3 'el 'R und x_1 <x_2 <x_3 haben.

Aufgabenstellung:

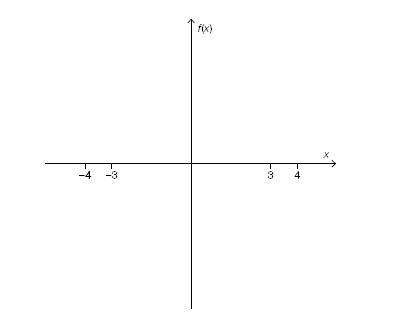
{{Grafik: Koordinatensystem:

waagrechte Achse: x;

senkrechte Achse: f(x);

---

Auf der waagrechten Achse sind die Werte -4, -3, 3 und 4 markiert.}}

---

Skizzieren Sie im nachstehenden Koordinatensystem im Intervall [-4; 4] den Verlauf des Graphen einer solchen Funktion f mit allen drei Nullstellen im Intervall [-3; 3]!

{{Beschreiben Sie den Verlauf des Graphen einer solchen Funktion.}}

[]

-----