Beispiel 086 - Einander schneidende Geraden: Unterschied zwischen den Versionen
| Zeile 31: | Zeile 31: | ||
==Aufbereitet== | ==Aufbereitet== | ||
<div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | <div style="background-color: #DBE5F1; padding: 5px 15px; font-family:Courier; font-size:12px; line-height: 150%;"> | ||
| − | {{Grafik: | + | {{Grafik: Koordinatensystem |
| − | |||
| − | Koordinatensystem | ||
waagrechte Achse: x; [0; 6], Skalierung: 1; | waagrechte Achse: x; [0; 6], Skalierung: 1; | ||
Version vom 7. April 2022, 08:04 Uhr
Übungstyp und Quelle
- Übungstyp
- Ausfüllen
- Vorhandene Inhaltstypen
- Informationsgrafik
- Vorhandene Strukturelemente
- -
- Aus dem Schulbuch
- Matura AHS Jänner 2020 Beispiel 7 (matura.gv.at - Mathematik)
- Seite(n)
- -
Original
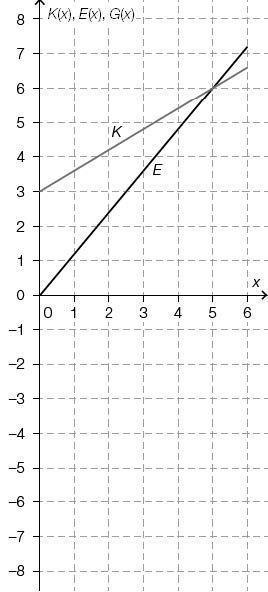
Die unten stehende Abbildung zeigt eine lineare Kostenfunktion K: x -> K(x) und eine lineare Erlösfunktion E: x -> E(x) mit x 'el [0; 6]. (Abb. 7)
Für die Gewinnfunktion G: x -> G(x) gilt für alle x 'el [0; 6]: G(x) =E(x) -K(x).
Aufgabenstellung:
Zeichnen Sie in der nachstehenden Abbildung den Graphen von G ein.
Aufbereitet
{{Grafik: Koordinatensystem
waagrechte Achse: x; [0; 6], Skalierung: 1;
senkrechte Achse: y; [-8; 8], Skalierung: 1;
---
Der dargestellte Graph von K ist linear steigend durch die Punkte (0|3) und (5|6).
Der dargestellte Graph von E ist linear steigend durch die Punkte (0|0) und (5|6).}}
---
Für die Gewinnfunktion G: x -> G(x) gilt für alle x 'el [0; 6]: G(x) =E(x) -K(x).
---
Aufgabenstellung:
Zeichnen Sie in der nachstehenden Abbildung den Graphen von G ein.
Alternativ: Beschreiben Sie den Graphen G und geben Sie charakteristische Wertepaare an.
[]
-----